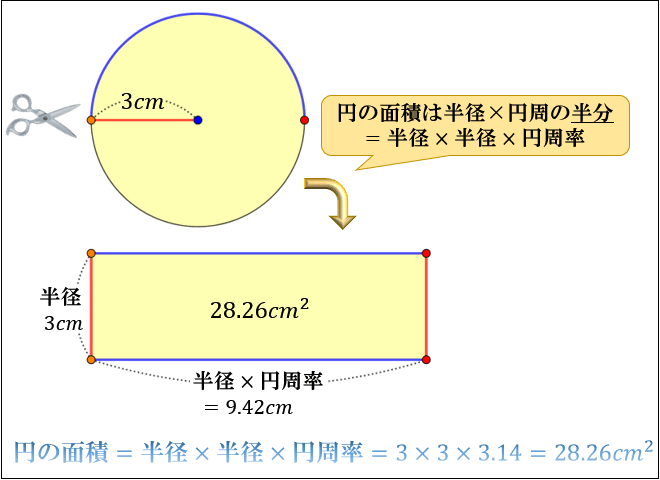
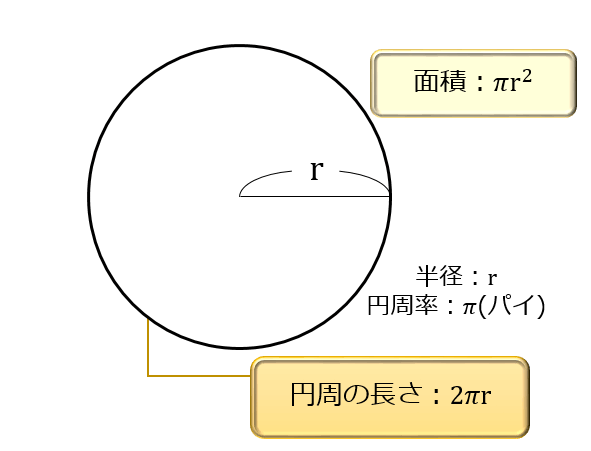
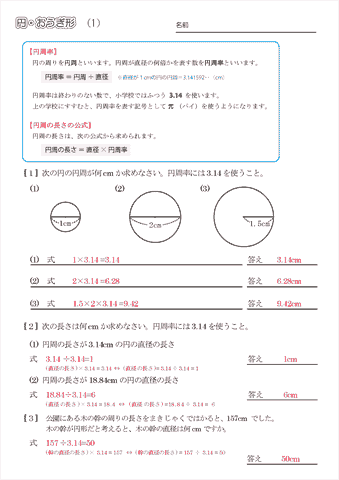
質問の答えとしては、円の面積を微分すると、 円周になると考えるのでなく、 円周の長さ2πx を0からrまで積分すると、 円の面積を表すのです。 次は、球の体積に移ります。 これも、授業ではタマネギの表皮を一枚一枚はがして、 生徒には説明します。 (臭いは相当なものがあります 2円の面積の公式 円周の公式同様、「半径⇒ r r 」「円周率⇒ π π 」と変換して文字式のルール通りに円の面積の公式も表します。 『半径×半径×314 × 314 』⇒『πr2 π r 2 』円でも,円周率は約314です。 また,円周率を使って,直径から円周の長さを求める式を考えると,円周÷直径=円周率 だから, 円周=直径×円周率 =半径×2×円周率 となります。 次の円の円周の長さは何cmですか。ただし,円周率は314とします。

円 扇形 の面積 周や弧の長さの公式 数学fun
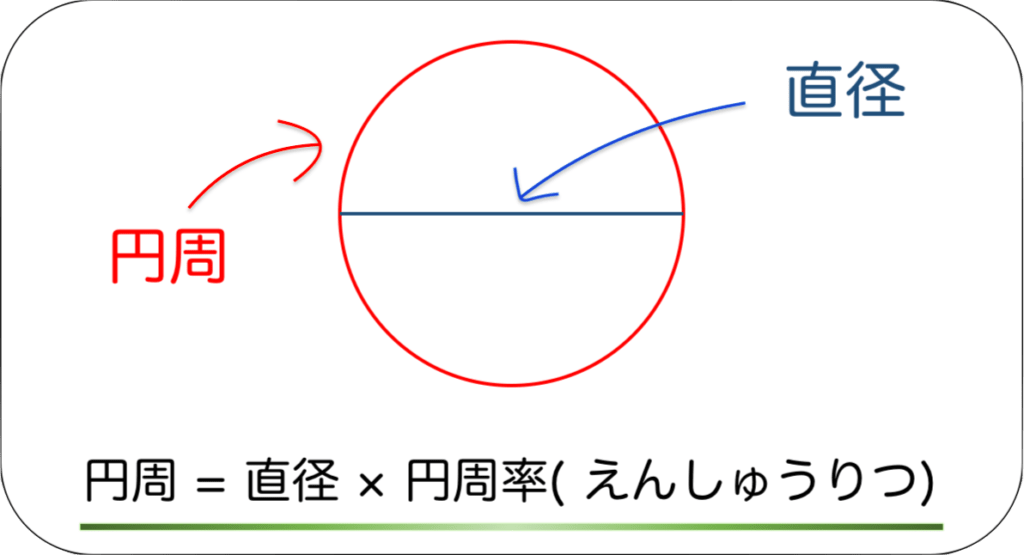
円の円周の長さ 公式
円の円周の長さ 公式- 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン弧の長さと面積の公式 <証明> 弧の長さと面積の公式の証明をしておきます。 証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。



直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ
L=∫{ 1+(dy/dx) 2 } 1/2 dx (曲線の長さを求める一般式) となります。それでは、上の公式を使って円の周長を計算してみましょう。 円の方程式: x 2 +y 2 =r 2 上式の両辺を微分して、 2x dx+2y dy=0 → dy / dx=-x / y円周の公式|なぜ直径×円周率で計算できるのか&円周率を 直径から計算!「円周の長さの求め方」の公式を3秒で覚える 扇形の弧の長さの求め方 公式と計算例;円の円周を計算する方法 円周の計算方法を知っておくと、手芸や工作をする時やジャグジーのまわりに柵を建てる時、また学校で単に数学の問題を解く時など、円を扱う様々な場面で重宝します。 直径を使って円周を計算する公式を書きます。公式は単純に C = πdです。
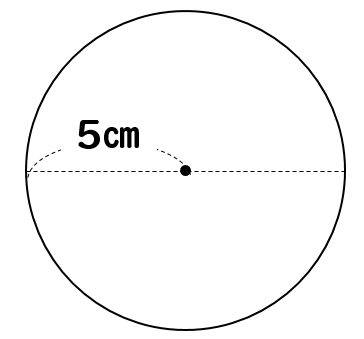
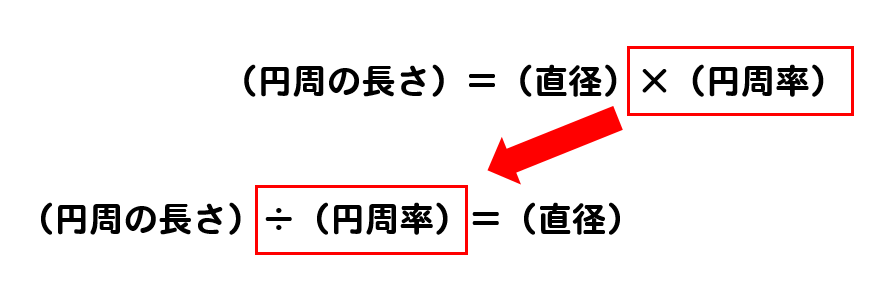
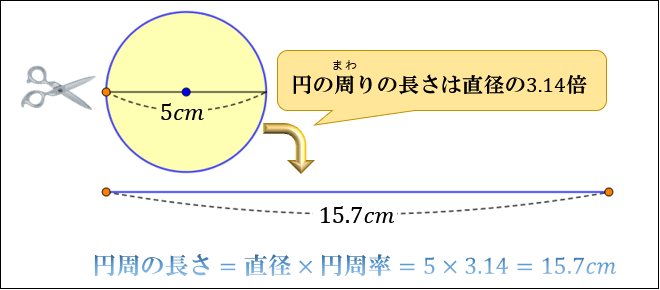
今ちょうど2乗に比例の式をやっている3年生ですが、高校見学に行った際、数学の授業でグラフに円が書いてあって『何これ面白そう』と思い"円 グラフ 式"と検索し調べていました。他のサイトはどこも高校生向けというか、難しく中学生の私にはわかりませんでした。 しかしここのサイト円周 ÷ π ÷ 2 で求めることができます。 円周 : 半径 : π(円周率)= 円周から半径を求める 円周から直径を求める 円周から面積を求める 円の面積から半径を求める 円の面積から直径を求める 円の面積から円周を求める 直径 × 円周率 = 2 × 半径 × 円周率 = 円周の長さ 円の半径を r としたら、その2倍が直径 2r 。 ですから、円の直径(2r)に円周率(π≒314)をかけることで円周の長さ(2πr ≒ 628r)が求まります。 例題①:半径5cmの円の、円周の長さを求めて下さい。
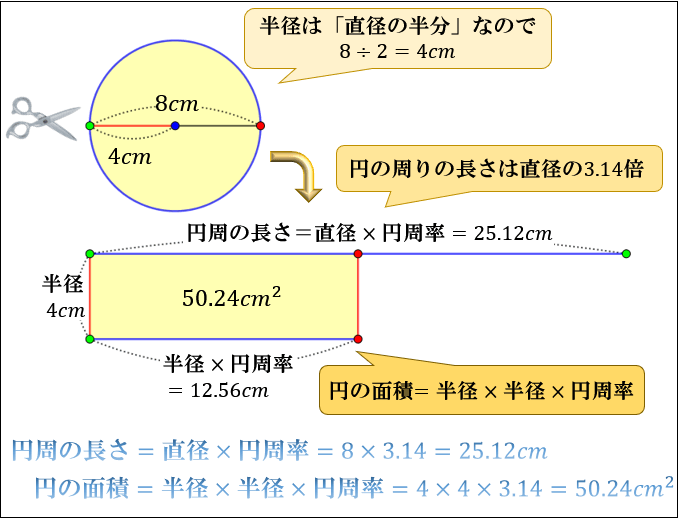
円周の長さを求める公式ってなんだっけ? そもそも、円周率ってなんだ? 計算方法ができない そういった悩みが解決できるように解説していくのでこの記事を通して理解を深めていきましょう(^^) Contents 円周率とは;円 の 長 さ を 求める 公式; 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の




正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support



円周の長さの問題をもっと解いてみよう 家庭学習レシピ
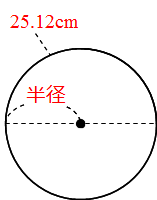
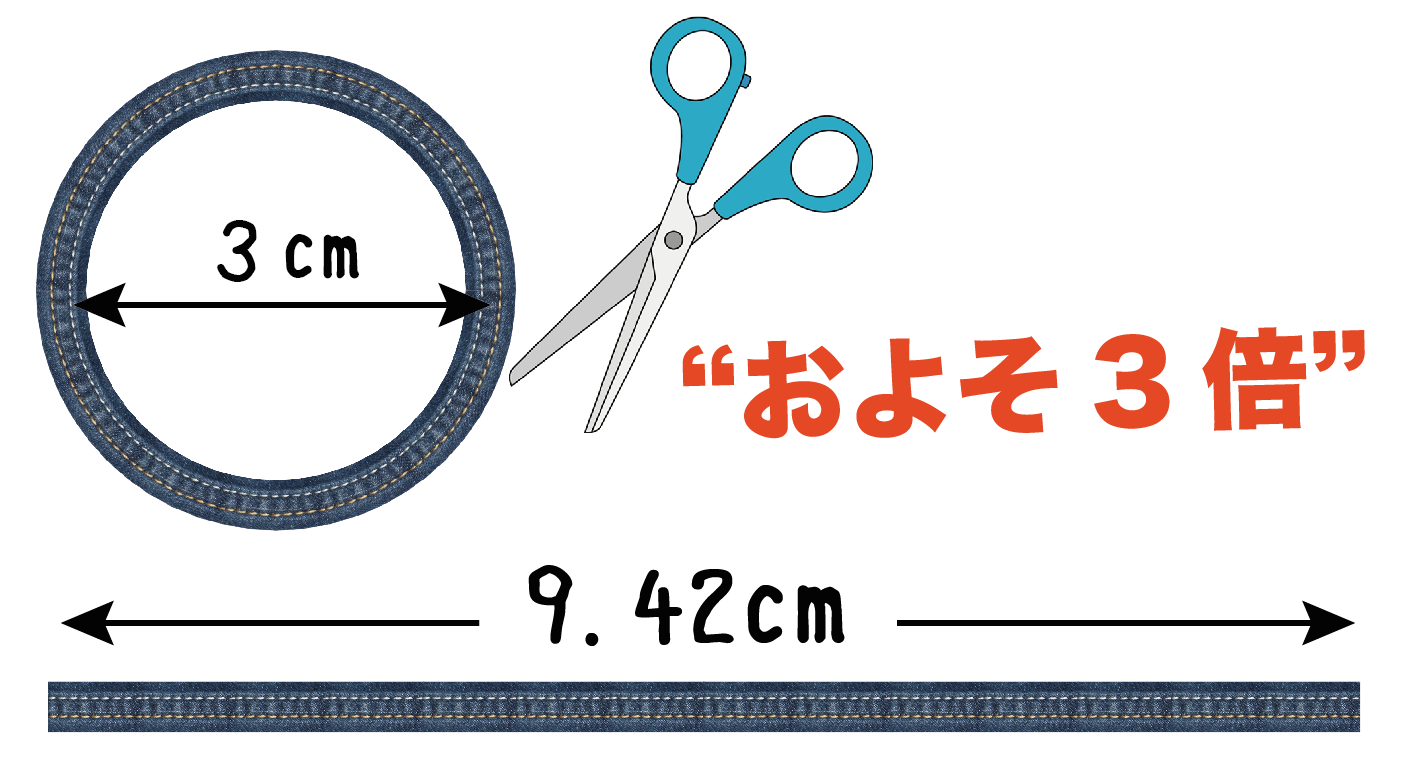
円周の長さは 直径×円周率=円周の長さ で求めることができます。 直径3cmの円周の長さは何cm? ※円周率を314でおこなう場合 → 3cm×314 → 942cm ※円周率をπでおこなう場合 → 3cm×π → 3πcm ひっかけ問題では、直径ではなく半径で出題されることが円弧の長さ 一つの円が与えられて、その周上の2点A、Bを結ぶと弦ができる。ここでは、その弦に 対する弧の長さについて知られていることをまとめることにしよう。 左図のように、円の半径 r と中心角 θ が与えられていれば、 弦の長さ a は、 2r・sin(θ/2) 弧の長さ L は、 rθ である12 円の面積の公式{その1{まず,円の面積の公式について考察してみる.円周率の定義によって,半径rの 円の周の長さは2ˇr である.その円の面積はˇr2 で与えられることは,次のよう に説明されている.円周を2n等分する.これを2n個の扇形に切って,それを2つ



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




16cm Descubre Como Resolverlo En Qanda
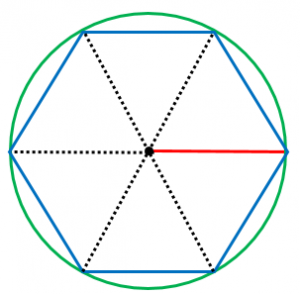
多角形による円周率の近似 正多角形の角の数を増やしていくと、形が円に近付いていく。 次の図では、角の数を6から24に増やすだけで、かなり円に近付くことがわかる。 このとき、正多角形の辺の長さの合計値も、円周の長さに近づくことになる。扇形の弧の長さ( l ength) π 円周率(= 314) r 円の半径( r adius) x° 中心角 公式の導き方 この公式は暗記するようなものではなく、意味を理解することに意味があります。この公式の意味は、円の面積に「360° に対する中心角の割合をかける」ことに方 べきの 定理とは, 平行でない 2 本の直線と円とが交わって(接して)できる図形の辺の長さの関係 を示している公式です。基本的には 3 つの形があります。 どれも三角形の相似から証明することができます。 ① 2 つの直線の交点が円の内部にあるとき このとき, が成り立ちます。




直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




円周率 算数用語集
〔質問〕 円の半径・円周、おうぎ形の弧の長さ・面積、円柱・円錐の面積、球の面積など複雑な公式が多くて、なかなか全部覚えられません。なにかいい覚え方はありますか? 〔回答〕 「丸暗記」する項目と、そこから「その都度導き出す★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料の長さと,胴回り(円の円周)の長さではど ちらが長いか」を確認するように指示した。 ・児童は,各自でリボンを使って確かめていた。 作業の様子をみると,リボンに印を付けて, 高さと円周を比較している児童も多かった。



東大入試解説 円周率が3 05よりも大きいことを証明せよ



半円の周の長さの計算方法 白丸くん
円周 率π について もう少し詳しく説明すると、扇形の面積の公式 扇形の面積= (弧長 £ 半径)¥2 を導く際に、lim θ!0 sinθ θ = 1 という事実を用いているところにある。証明しよ うとしている事柄を用いて得られる事実は、その事柄自体の証明では使って はいけないのである。中学校で習った 一方(円の周の長 さ a = b a=b a = b のときは ϵ = 0 \epsilon=0 ϵ = 0 , L = 2 π a L=2\pi a L = 2 πa となり円周の長さの公式 と一致します。 楕円の周の長さの導出 冒頭の公式を3段階に分けて証明します。3つの道具を知っていれば簡単です! 1.周長をとりあえず積分で書き下す。 使う道具:弧長積分本ライブラリは会員の方が作成した作品です。 内容について当サイトは一切関知しません。 円のまわりの長さ のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



5分でわかる 円周の求め方の公式 計算例を京大生がイラスト付きで説明します
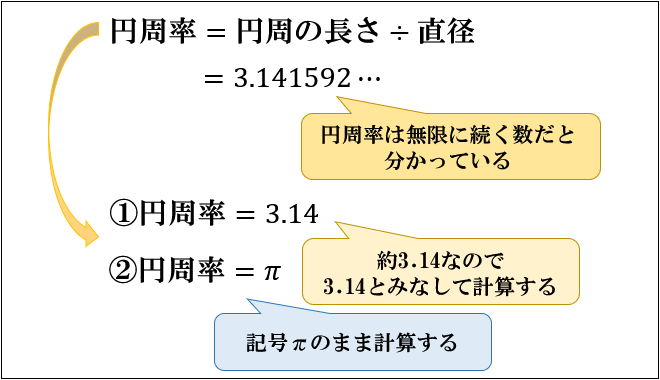
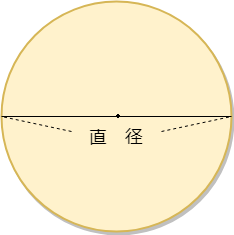
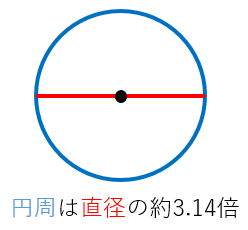
正方形の周りの長さの求め方は?1分でわかる長さ、長方形の周りの長さ 円の直径、円周とは?1分でわかる意味、円周や断面積から半径、直径を求める 半径の求め方は?1分でわかる方法、公式、円周との関係、扇形の円弧から半径を求める方法 管理人おすすめ!セットで3割もお得!大 円周率はどんな円でもかならず同じ数(\(314\))になります。 すなわち、円はかならず「直径を314倍すると円周の長さ」になるのです。 円周率 円周の長さが直径の何倍であるかを表す数 円の面積の公式の求め方 では、本題に入りましょう。なぜ円の面積円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き 円の面積 面積;




円周の求め方 公式と計算例




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題
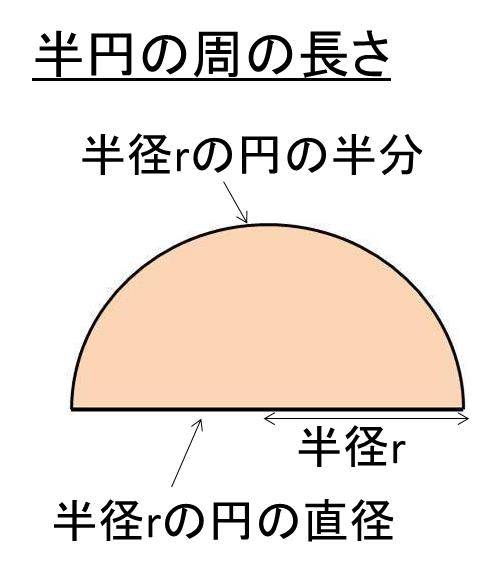
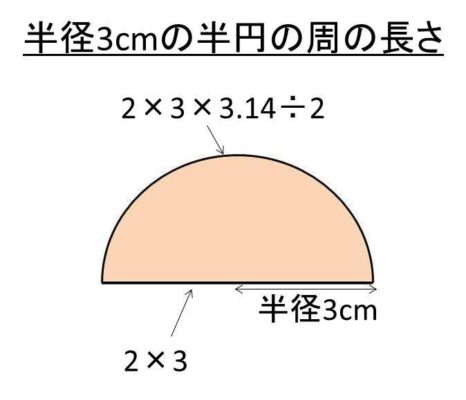
正多角形と円/理解シート 円周から,直径・半径を求める方法を教えて 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO Created Date 926 PM つまり、 半円の周長=半径rの円の半分+半径rの円の直径 という計算式が成立するわけです。 ここで、半円の円形状の長さは半径rと円周率314を用いると、2×r×314÷2となります。 また、直線部分の長さは2×rと記載することができます。楕円の円周を計算するための高精度の単純な式はありません。 以下は、この計算機で使用される楕円の円周の近似計算式です。 ここで: a =楕円の半長軸の長さ b =楕円の短短軸長 π=




直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ



円周の求め方と円の面積について アタリマエ
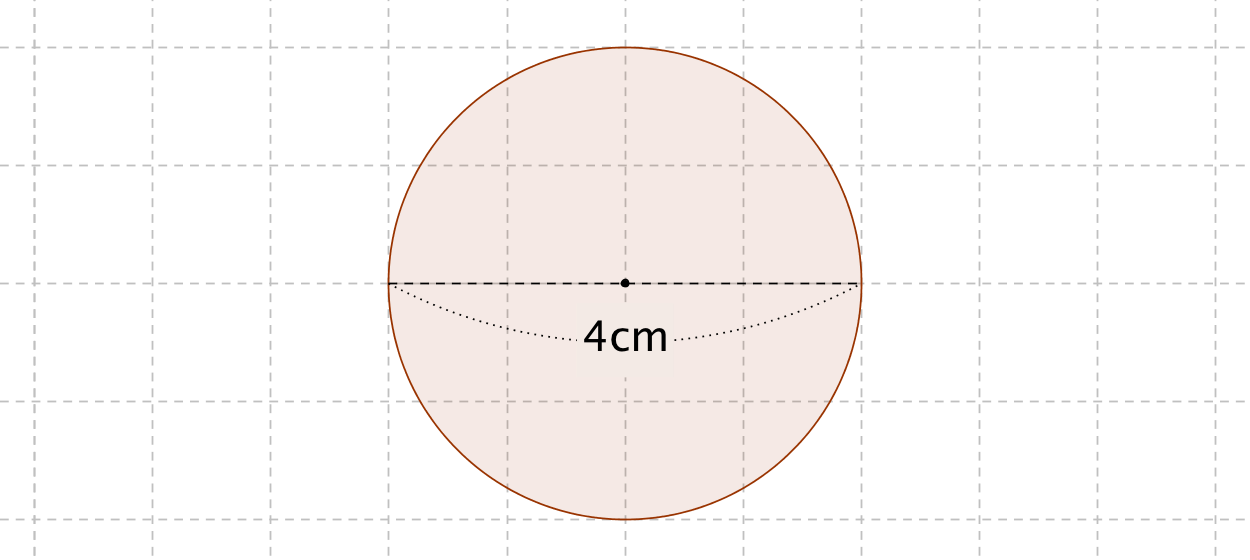
円周を求める公式 円周は『直径×円周率』で計算できます。 小学校算数では円周率を 314 314 としているので、円周は 『直径×314 × 314 』 です。 たとえば以下のような問題の場合。 例題 直径 4cm 4 c m の円の円周を求めよ。 答えはこのように求める直径から計算 直径: 面積: 半径から計算 半径: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形物理公式集 円周率 cm;



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau




円 扇形 の面積 周や弧の長さの公式 数学fun




円の面積 円周の求め方 公式 小学生 中学生の勉強



円周の公式 算数の公式




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun



直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



円周の求め方と円の面積について アタリマエ



半円の周の長さの計算方法 白丸くん




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




小学生でもできる円周率の求め方 いろいろな方法を紹介 数学の面白いこと 役に立つことをまとめたサイト



直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題



円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ
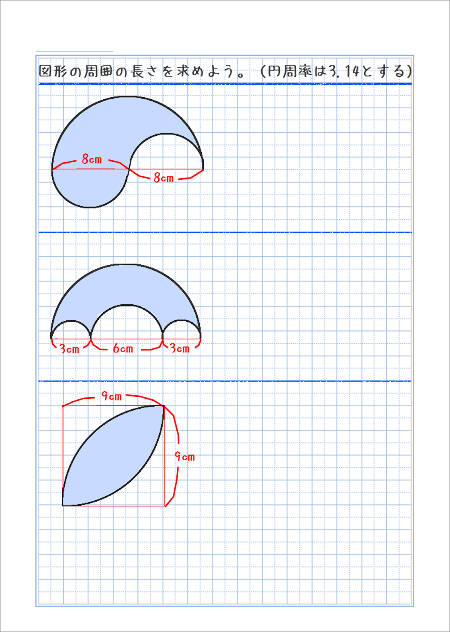



円周の長さの問題をもっと解いてみよう 家庭学習レシピ




円の面積 算数用語集




小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生



世界一やさしい 円周率と 円周を求める問題の解き方 働きアリ




扇形の弧の長さの求め方 公式と計算例




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
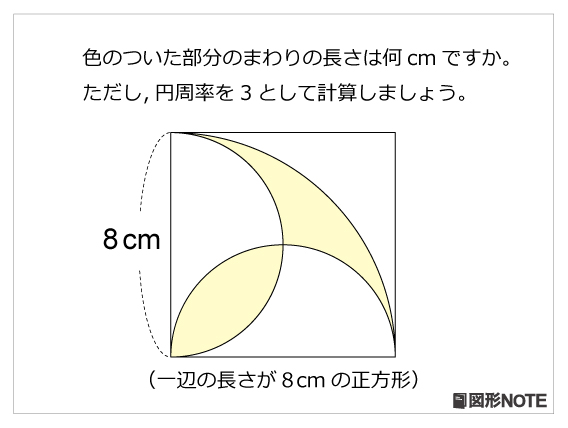



図形noteプレ レベル4 まわりの長さ 算数星人のweb問題集 中学受験算数の問題に挑戦



エッセイ68 パパの夏休みの宿題 円周率p パイ




周りの長さ 半円 Youtube




円周と円周率 面積 表面積 体積の求め方について基本を解説 高校生向け受験応援メディア 受験のミカタ



円周率 P とは 求め方や100桁までの覚え方をご紹介 受験辞典




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



5年算数 円と正多角形 2 わかる教え方のポイント



小学生算数問題です 解説解答宜しくお願いします 半径が8 の半円のまわりの Yahoo 知恵袋




円の周りの長さを計算しよう 家庭学習レシピ



円の面積 円周の求め方 公式 小学生 中学生の勉強



円周の求め方と円の面積について アタリマエ



小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生




小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生



円周の長さの求め方と例題 具体例で学ぶ数学
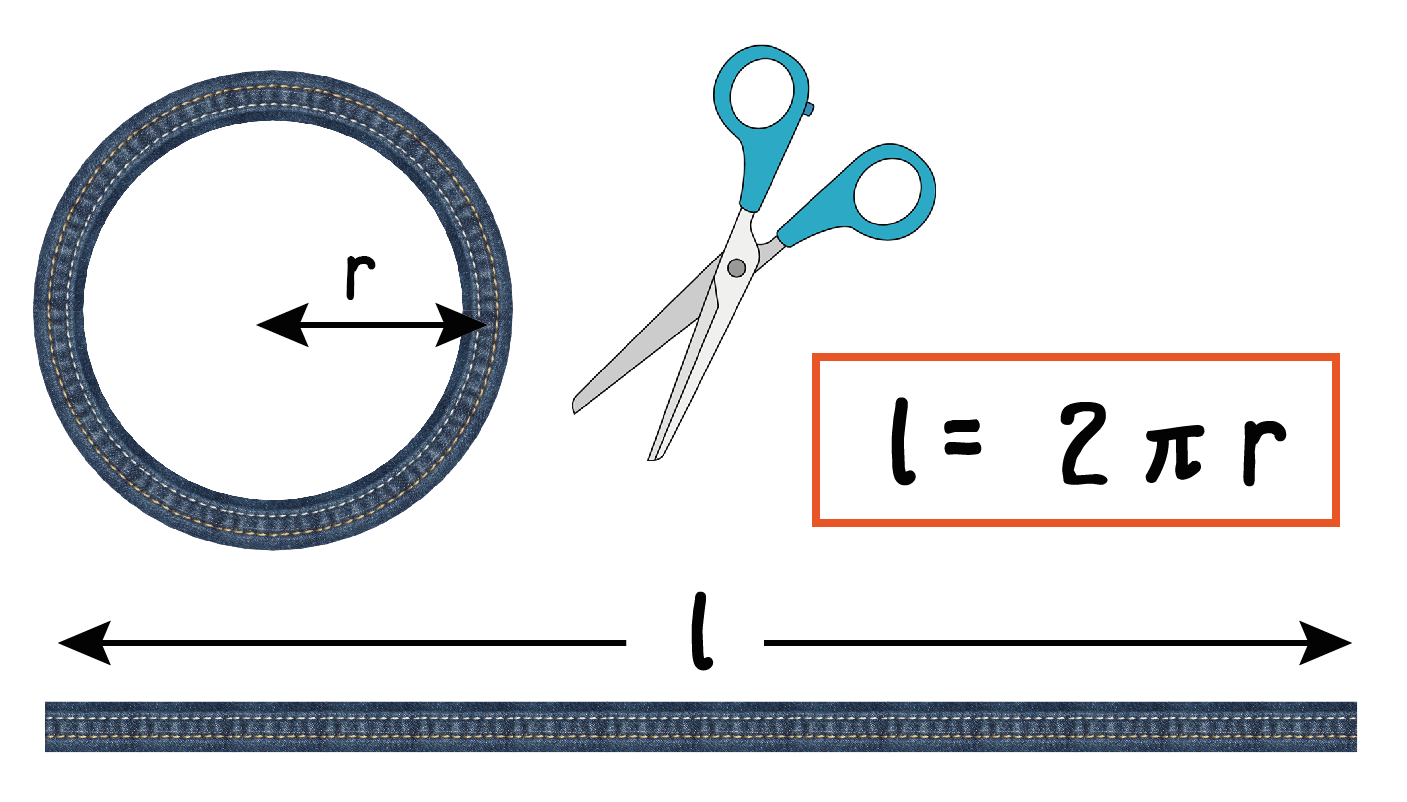



直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく




円の面積の求め方を自主学習ノートで復習しましょう 円の面積の基本的な練習問題 円の面積の求め方を確認しておきます 円の面積 半径 半径 円周率 ちなみに 円周の長さの求め方は 学習ノート 数学ノート 学習



円周の求め方と円の面積について アタリマエ




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




円周率の意味って何 Pの意味を分かりやすく説明します 数学の面白いこと 役に立つことをまとめたサイト



Q Tbn And9gcqyrslclwl4zjqsiu Eb80r3ccsntxpibvziibi Muwysoknwz Usqp Cau




円周の求め方 公式と計算例




分かりません 教え下さい 明日までにお願いします Clear




1分でわかる 円周の長さの求め方の計算公式 Youtube



円周の長さの求め方と例題 具体例で学ぶ数学




円周から直径を求める Youtube



直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく
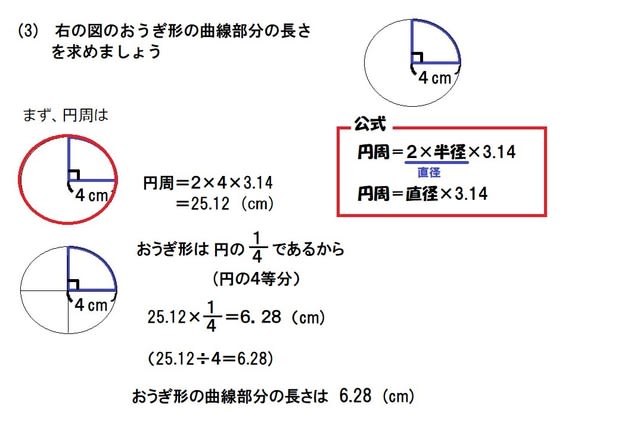



正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support




円の面積 円周の求め方 公式 小学生 中学生の勉強




教えてください どうしても分からないんです 教えてください Clear




円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ



1



円周の長さの問題をもっと解いてみよう 家庭学習レシピ




14cm 14cn Descubre Como Resolverlo En Qanda




小学5年生 円周率 円のまわりの長さ 算数 Active Learning 学院




正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support



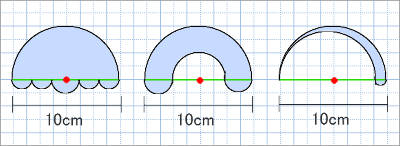
世界一やさしい 円周率と 円周を求める問題の解き方 働きアリ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun




円の面積 円周の求め方 公式 小学生 中学生の勉強




円周と円周率 面積 表面積 体積の求め方について基本を解説 高校生向け受験応援メディア 受験のミカタ



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




円周の求め方と円の面積について アタリマエ




分からないので式と答えお願いします Clear




円周の求め方と円の面積について アタリマエ



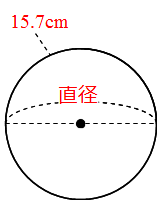
小5 算数 小5 55 円のまわりの長さ Youtube
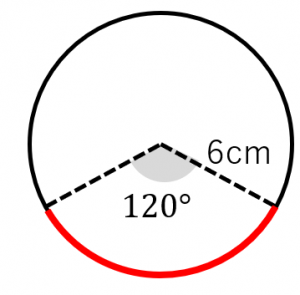



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




色がついてる部分のまわりの長さの求め方を教えて下さい よろしくお願いします Clear




円周 の長さ 計算ドリル 問題集 数学fun




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun




小学5年生 円周率 円のまわりの長さ 算数 Active Learning 学院



円周怪獣ラジアン 14 1改訂版 ラジアン Rad は量の単位としてはやや特殊なものです これは 同じ中心角の円弧 円の一部 の長さと半径 の長さの比率は常に一定である という原理に基づいた単位だったりします 何のこっちゃ という感じ
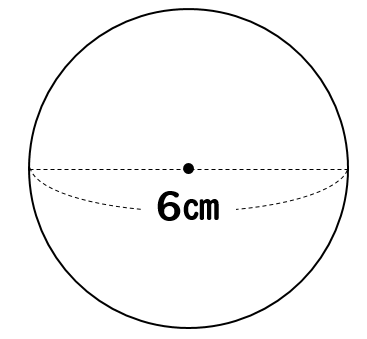



直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




円の周りの長さを計算しよう 家庭学習レシピ



1
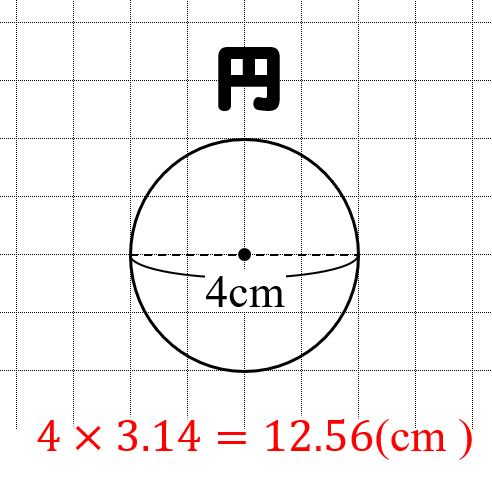



円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun
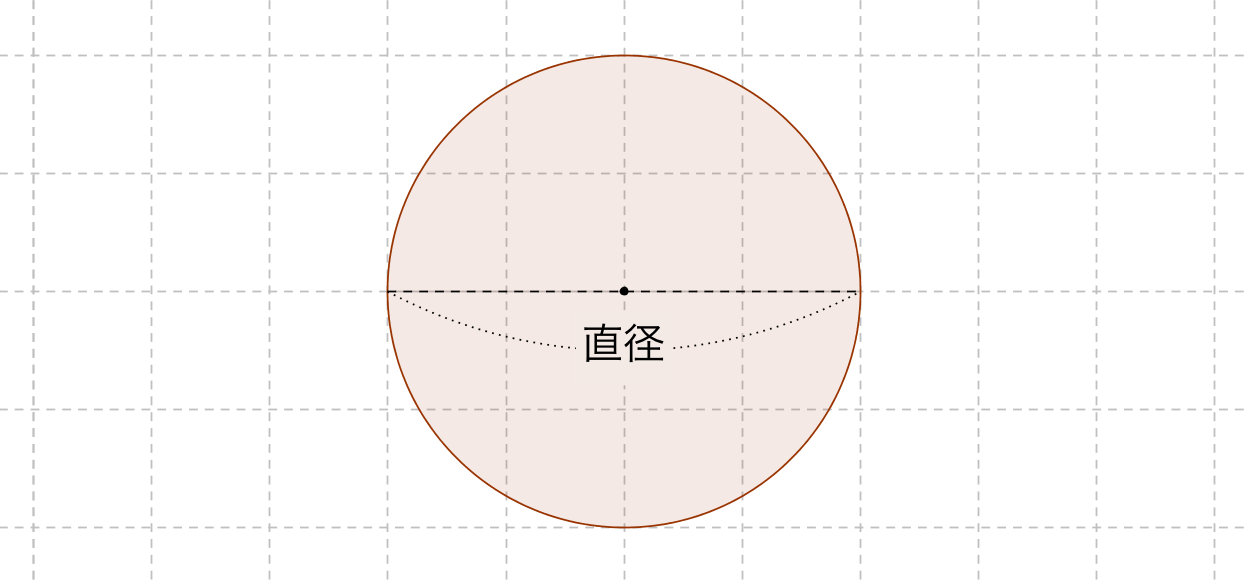



円周の公式 算数の公式
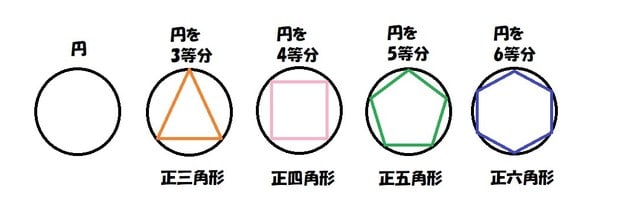



正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
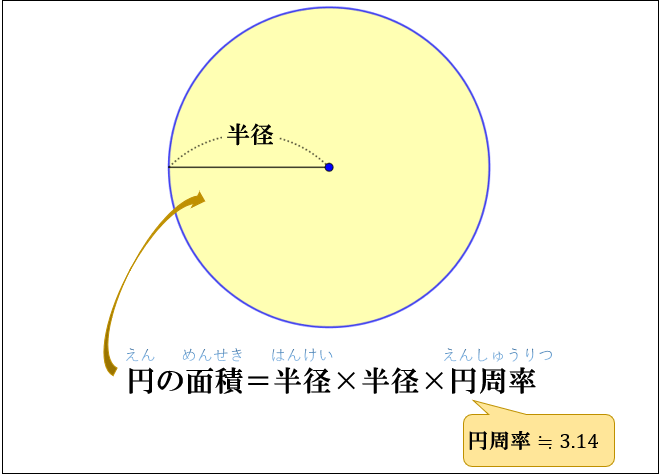



円周の求め方と円の面積について アタリマエ
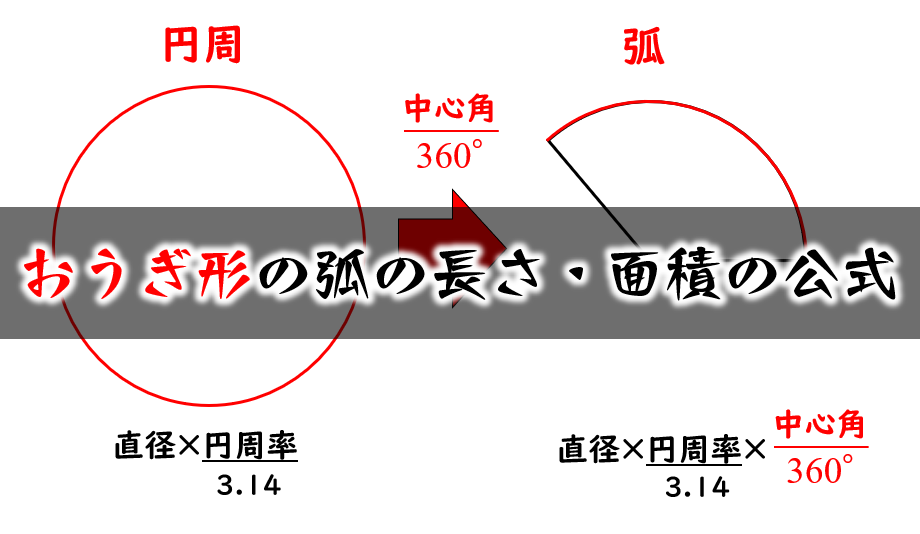



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




円の面積 円周の求め方 公式 小学生 中学生の勉強




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




小学生でもできる円周率の求め方 いろいろな方法を紹介 数学の面白いこと 役に立つことをまとめたサイト
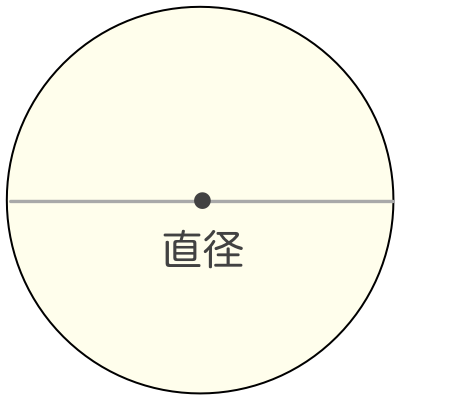



円周の長さ 簡単に計算できる電卓サイト




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円 扇形 の面積 周や弧の長さの公式 数学fun



あとまあく数学の演習 円周小5以上
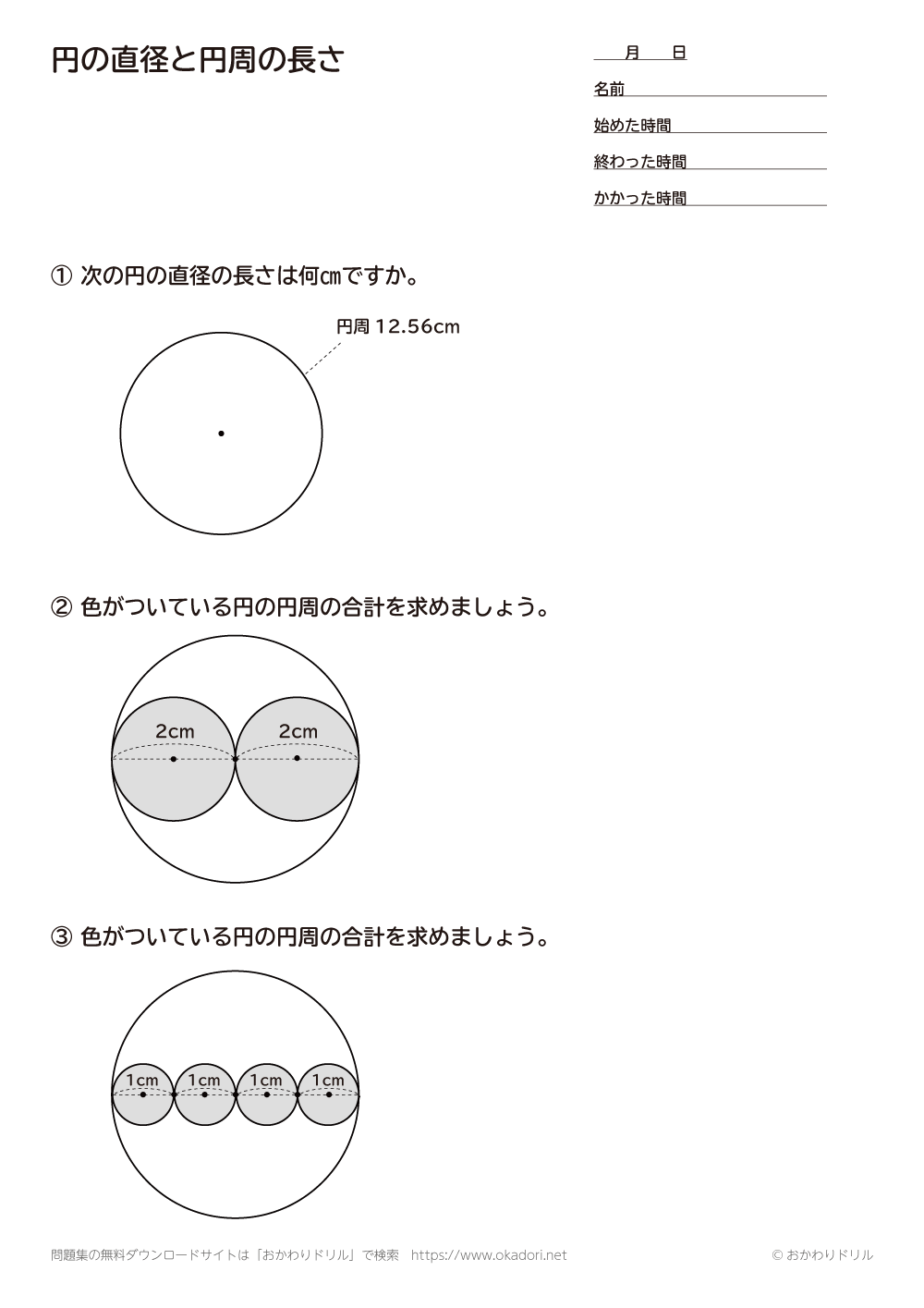



小学5年生 算数 無料問題集 円の直径と円周の長さ おかわりドリル



0 件のコメント:
コメントを投稿