球の表面積は S = 4πr2 S = 4 π r 2表面積(側面積)+(底面積)×2=80∏+25∏×2=130∏ (cm2) 答 体積 0∏ cm 3 ,表面積 130∏ cm 2 131 右の図は,三角柱とその展開図である。 円柱の体積の公式である底面積×高さと一致することが分かります。 三角錐 次は下の図のような三角錐の体積\(V\)を求めてみたいと思います。 まず積分する方向を今回は\(z\)軸方向と決めたいと思います。よって\(z\)は0から1の範囲で積分することになります。
1
面積と体積の公式
面積と体積の公式- 2 体積 立方体 = 一辺 × 一辺 × 一辺 直方体 = 縦 × 横 × 高さ 柱体 = 底面積 × 高さ 3 角度 三角形の内角の和 = 180度 四角形の内角の和 = 360度 多角形の内角の和 = 180度 ×(頂点の数-2) 4 円 円周率 = 3.14 円 周 = 直径 × 円周率 A 体積96π( c m 3 )・表面積96π( c m 2 ) 円錐の体積の公式は 「底面積 × 高さ × 1 3 」でしたね。 よって、式は 6 × 6 × π × 8 × 1 3 = 96 π 円錐の体積は、 96( c m 3 ) となります。 続いて表面積です。 円錐の表面積の公式は 「底面積 側面積」でしたね。 底面積は6 × 6 × π = 36π とすぐに出せますね。 続いて、 円錐の側面積の求め方は 「半径 × π
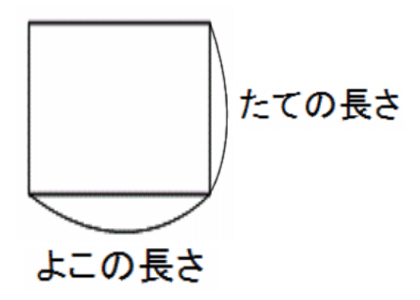



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
そして、底面積×高さ(h)=円柱の体積ですから、「36π×13=468π(cm3)」が答えです。これを公式化すると下のようになります。公式円柱の体積=底面積×高さ =半径×半径×円周率×高さ =πr2h =Shちなみに円錐の体積を求める公式もあります。面積と積分の関係は? 積分は、ある線分、微小面積などの「総和」を意味します(※数学的な意味では無いです)。総和とは、「合計」のことです。下図をみてください。四角形(図形A)があります。 私たちは、四角形の面積の公式が、 面積=a×b 次に,底面積が S S S ,高さが h h h の一般の錐体 A A A の体積 V V V について考えます。 底面が一辺 2 h 2h 2 h の正方形であるような特殊な四角錐 B B B の体積は 1 3 S B h \dfrac{1}{3}S_Bh 3 1 S B h でした( S B = 4 h 2 S_B=4h^2 S B = 4 h 2 は B B B の底面積)。
それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 ( c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 ( c m 3) つづいて、立方体・直方体がこれらの公式で求められる理由について説明していきます。 この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 断面積の積分や回転体の体積 21年2月19日 この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。 各種公式や問題の解き方なども説明していくので、ぜひこの記事を通してマスターしてくださいね! 目次 非
体積・表面積 立方体の辺の長さから体積と表面積を計算します。 立方体の体積から辺の長さと表面積を計算します。 直方体の三辺の長さから体積と表面積を計算します。 四面体の6つの辺の長さから体積と表面積を計算します。 正四面体の辺の長さから体積と表面積を計算します。 正四面体の体積から辺の長さと表面積を計算します。 正三角柱の底辺と高さこの場合,回転体は半径2cm,高さ4cmの円柱になるので,その体積Vは V=底面積×高さ=2×2×π×4= 16π cm 3 となります. これをパップス・ギュルダンの定理を使って解いてみます. 「 断面積 」は縦4cm,横2cmの長方形なので 2×4=8 cm 2 です. 「 断面の底辺の長さ $a$、高さ $h$ の平行四辺形の面積 $S$ は、次の公式で求められます。 平行四辺形 (へいこうしへんけい) の面積 \begin{align*} S = ah \end{align*} 面積 = 底辺 × 高さ 公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「平行四辺形の面積の求め方」をご覧ください。



1
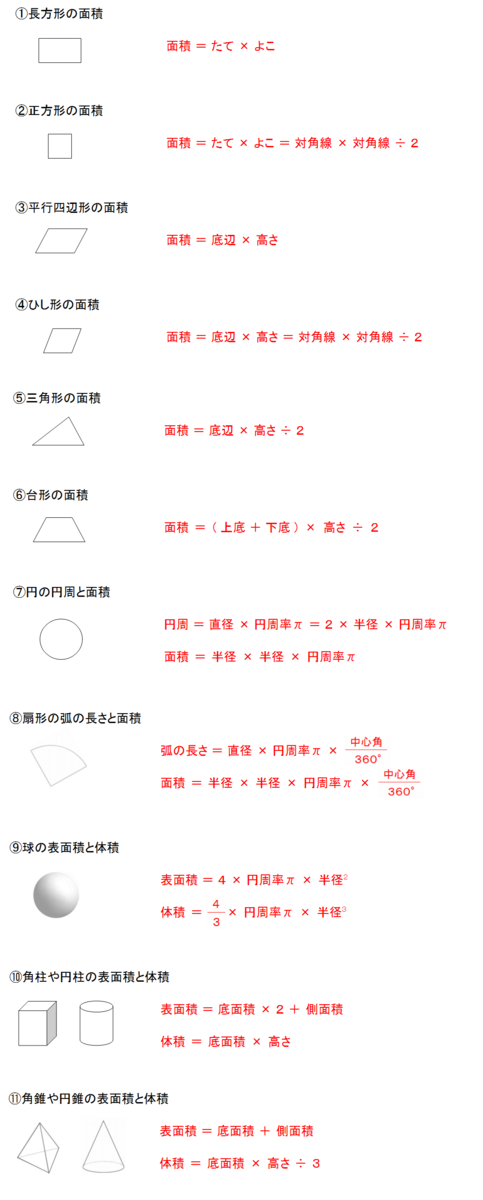



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
体積や面積を求めるとき、 公式が通用しないとき は 『 部分 』+『 部分 』 『 全体 』-『 部分 』 を利用することはよくあります。 これはその典型です。 表面積は簡単には求まりませんが、部分部分は難しくはありません。 まずは半球の表面部分、面積の基本①(x軸方向への定積分) 面積の基本②(y軸方向への定積分) 接線と面積, 接する2曲線と面積;三角錐や四角錐などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角錐 (かくすい) の体積 \begin{align*} V = \frac{1}{3}Sh \end{align*} 体積 = 底面積 × 高さ ÷ 3



6年算数立体の体積その2 教え方




球の体積と表面積 Youtube
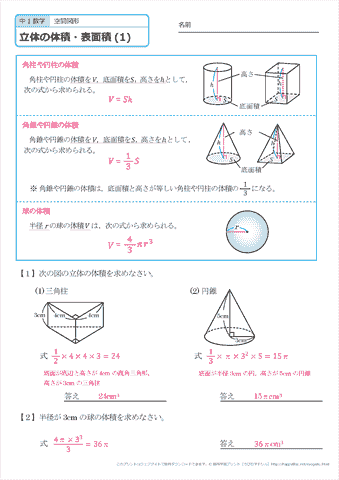
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題1立方体と直方体 立方体の体積=1辺×1辺×1辺 立方体の表面積=1辺×1辺×6 直方体の体積=たて×よこ×高さ 2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 角すいと円すいの体積=底面積×高さ× 球の体積の求め方(公式)の次は、球の表面積の求め方(公式)を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr2となります。 これもまた、球の表面積の公式がなぜ4πr 2 となるのか疑問に思う人もいるでしょう。



体積と面積の違いは 1分でわかる違い 意味 公式と求め方




体積の求め方 計算公式一覧
無料でダウンロード・プリントアウトできる小学生用・算数の単位換算表 です。 小学校で習う、時間、長さ、かさ、重さ、面積、体積の単位の一覧、早見表を作ってみました。 関連ページ ⇒小学6年生 いろいろな単位・単位の計算 問題プリント台形の高さ・面積 (4辺の長さから) 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 ひし形の面積 平行四辺形の面積 (底辺と高さから)例題2:半径が 2 c m の半球の表面積を計算してみましょう。 公式を使うと、 3 × π × 2 × 2 = 12 π c m 2 と計算できます。 円周率 π はおおよそ 314 なので、半球の体積はおおよそ、 12 × 314 = 3768 c m 3 となります。
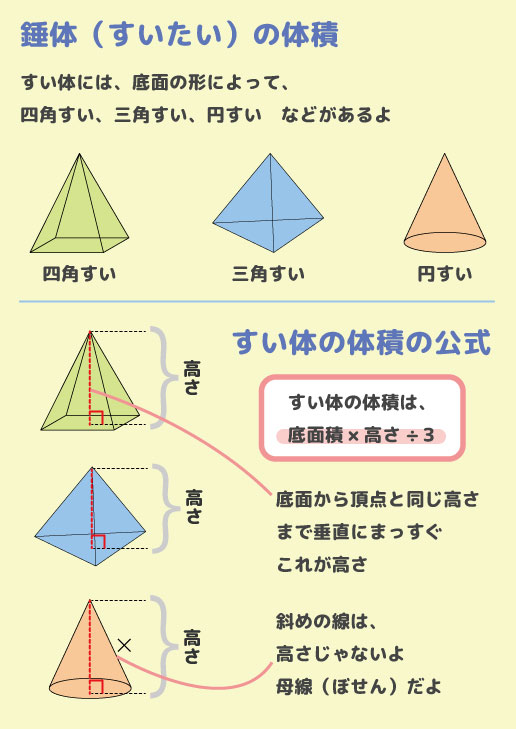



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強



1
面積 体積 公式 一覧35種類! 1 面積 正方形 = 一辺 × 一辺 長方形 = 縦 × 横 平行四辺形 = 底辺 × 高さ 三角形 = 底辺 × 高さ ÷ 22角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 高校入試対策数学 球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗 という公式はつぎの語呂を使えばおぼえられちゃうよ。 簡単公式台形の体積(正四角錐台)の求め方がわかる3ステップ 台形の体積の公式の求め方を知りたい!? こんにちは!この記事をかいているKenだよ。着る毛布ほしいね。 台形の体積の求め方 を教えてほしい。 そう、きかれることが結構ある。 正直



地図の体積計測




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ
立方体 = 一辺 × 一辺 × 一辺 直方体 = 縦 × 横 × 高さ 柱体 = 底面積 × 高さ 3平面図形 公式集 a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積ようするに,底面積と高ささえわかれば,円柱でも円すいでも簡単なかけ算で体積が求められるのですね。このポイントをおさえた上で,実際に問題を解いてみましょう。 関連記事 「おうぎ形の公式」について詳しく知りたい方はこちら 「円柱・円すいの表面積」について詳しく知りたい方は




単位の関係 長さと面積 Youtube




体積の求め方 計算公式一覧
曲線x a +y b =1の面積とベータ関数公式提示から実験で確認 球の表面積=円柱の側面積(アルキメデスの発見) 球の体積と表面積の関係から 球の表面積や体積を求める公式は,特に生徒が暗記に頼ってしまいがちな箇所ですが,暗記の覚 面積 \(\pi \times 3^2=9\pi (cm^2)\) 半径3㎝、中心角60°のおうぎ形の弧の長さ、面積 弧の長さ \(\displaystyle{2\pi \times 3 \times \frac{60}{360}=\pi (cm)}\)




小5 算数 小5 3 直方体と立方体の体積 Youtube




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p




公式を図解 すい体の体積 円すいの表面積の求め方




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




中1 数学 6 5 球の体積 表面積 Youtube



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



超簡単 体積の求め方 苦手な数学を簡単に




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




球の表面積と体積の公式 数学fun




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




球の表面積と体積の公式 数学fun




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




Amazon Music かっきー アッシュポテトの面積と体積 公式のうたなんです Amazon Co Jp
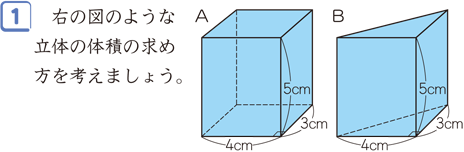



角柱と円柱の体積 算数用語集




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




体積 表面積




体積の求め方 計算公式一覧




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




Catatan Tentang 体積 表面積 側面積 の公式 Junior Clear




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




2 を途中式を含めて教えてください Clear




小学校6年間で習う 算数の公式一覧 無料学習プリント 計算問題無料印刷 Origami Project



角柱の体積は 1分でわかる公式 求め方 底面積 台形の関係




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球の体積と表面積 公式と計算問題と証明 Irohabook




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の公式 数学fun




公式を図解 すい体の体積 円すいの表面積の求め方



U9j580gf8iba369ji2w Xyz P 296




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




角錐 円錐の体積と表面積の公式 数学fun



1




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




体積の求め方 計算公式一覧




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
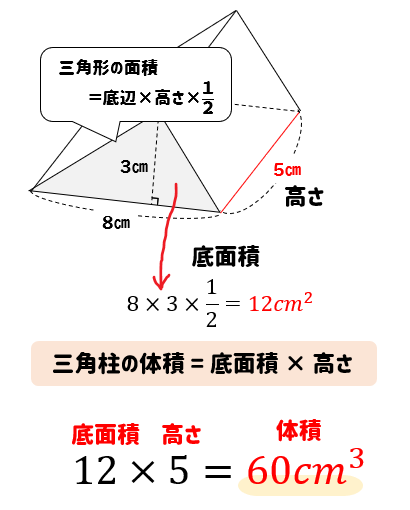



3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円柱の表面積と体積を求める公式 具体例で学ぶ数学




体積の求め方 公式一覧 小学生 中学生の勉強




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球に関する公式 理数系無料オンライン学習 Kori



1




高校数学 楕円の面積と回転体の体積 受験の月




球の表面積と体積の公式 数学fun




角柱 円柱の表面積と体積の公式 数学fun




体積の求め方 公式一覧 小学生 中学生の勉強




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



この四角柱の表面積と体積の求め方を教えて下さい 体積は 底面 Yahoo 知恵袋




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の体積ってなんであの公式なの Webty Staff Blog



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




円すいのときの体積の求め方の公式と 球の体積の求め方の公式を教えてください Clear
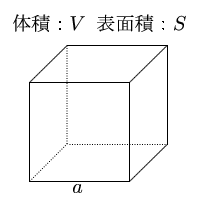



立方体の体積 表面積 体積 表面積の計算 計算サイト




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
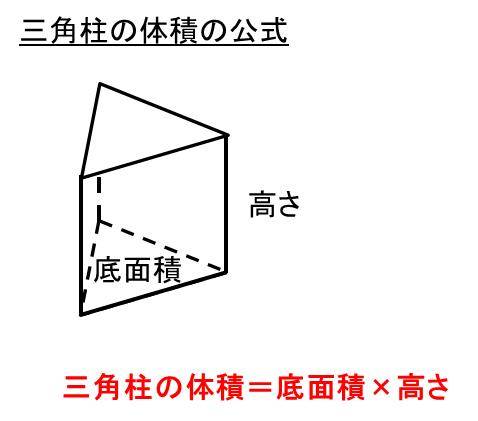



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム
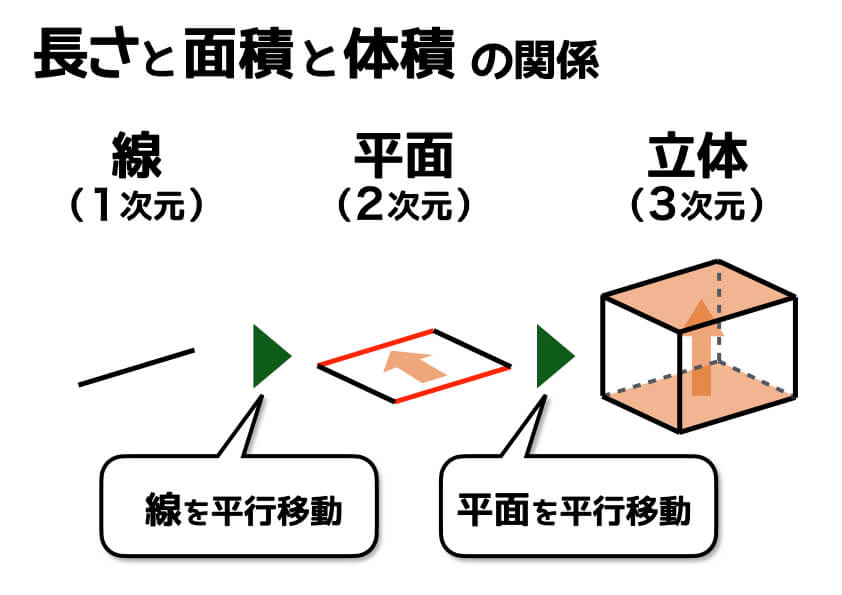



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




半球の体積と表面積を計算する 具体例で学ぶ数学




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu
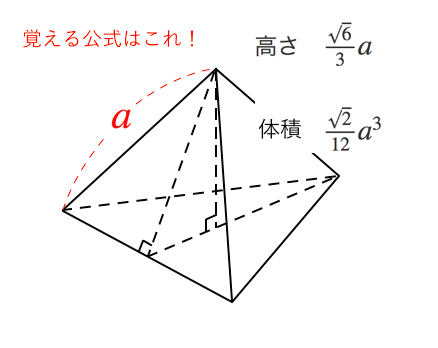



正四面体 高さ 面積を求める公式 苦手な数学を簡単に




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典
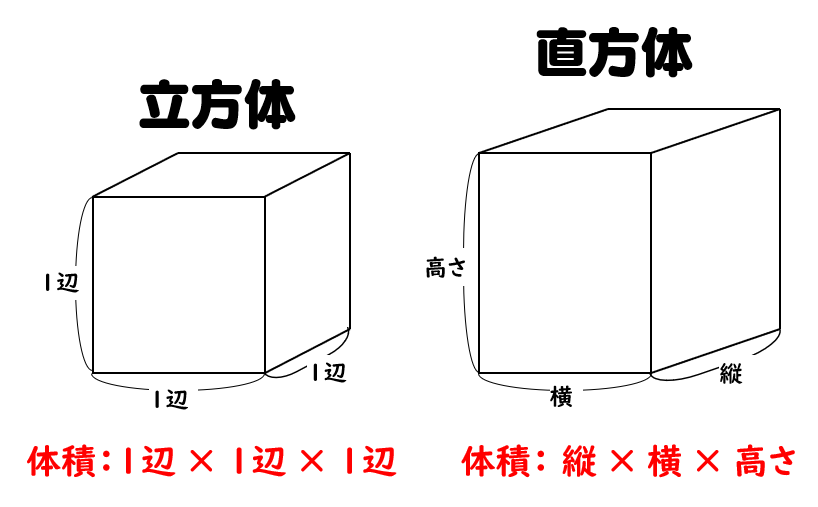



立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



体積計算機 断面積から体積計算 公式 求め方




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小5 算数 小5 5 体積の求め方のくふう Youtube




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




球の体積 球の表面積の公式の導出 積分 優技録




算数の公式 教育 プリントアウトファクトリー Myricoh



0 件のコメント:
コメントを投稿