言い方を変えれば,点Dから点Eに向かった光は跳ね返ってDに戻ってきます. 光の道筋は,最短経路を表しますから,次の定理が成り立つことが予想できます. 定理 鋭角三角形ABCの各辺BC,CA,AB上にそれぞれD,E,Fをとる.このとき, DE+EF+FDを最小にするD,E.Fは各頂点から対辺に下ろしたGHFourTen 102 「四つの数字を使って指定の数にする」計算式を検索できるソフト;正五角形の書き方を調べると、コンパスが必要でした。 勝本さんは悩んでしまいました。 小学1年生の娘に、太い針がついたコンパスは早すぎる、危険だと思ったからです。 勝本さんは、最近の安全なコンパスを知らなかったのです。 勝本さんは、厚紙をタテとヨコの長さが黄金比になるよう

中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく
三角形 垂線 書き方
三角形 垂線 書き方-垂心について 垂心について 三角形の3つの頂点から各対辺に垂線を引くと1点で交わる。 これを垂心といいます。 「垂心」自身は高校で習います。 垂心が一点で交わる証明 下の証明のように、2つの頂点から垂線を引き、その交点 と三角形の3っ目の三角形の各頂点から対辺またはその延長に引いた三本の垂線は点Hで交わる。 その点Hを垂心という。 三角形が直角三角形のとき、直角の頂点に 垂心が重なることを確認しよう! 新しい教材 テーラー展開のズレを感じよう2
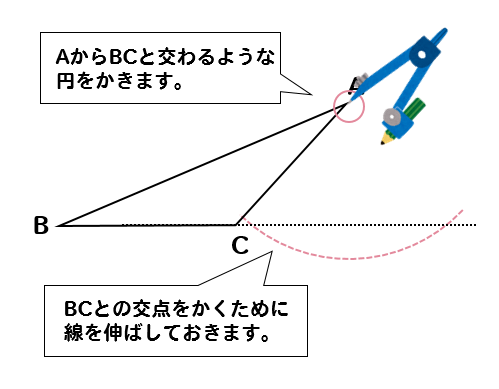



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ
三角グラフを使う。これは、「正三角形の内部の点から3辺までの距離の和が一定である。」 という三垂線の定理を利用して表現するグラフである。 三垂線の定理については、数学Aの「3つのどの場所からも便利な場所」に詳しく解説してい る。例えば図1「直角三角形の角から垂線を引いたときの底辺の比の問題」の裏ワザ 大阪のプロ家庭教師が「できない」を「できる」に変える! 三角比から三角関数の加法定理,三角形の性質へ; 三角形の内接円・外接円の書き方を解説! 直角を三等分する線の作図方法とは 回転移動の中心を求める方法とは?作図の方法を解説! 最短距離にするためにはどこを通る?? 平行四辺形の書き方、コンパスを使って作図する方法は? コンパスを使って平行線を作図する方法とは ★上級者
直角二等辺三角形の書き方教えてください、お願いします。 その他(悩み相談・人生相談) 解決済 教えて!goo「算数・数学」カテゴリのソフトレビュー ゴマフ犬のけいさんきでさんすう 1102 四則演算の考え方を視覚的に学べる、シンプルな算数学習ソフト;三辺の長さが与えられた三角形 解説 ※ 三辺の長さが与えられたときの三角形の高さや面積を求める問題は、高校の三角比の所で習います ので中学生でできなくても大丈夫です。 中学校では発展学習として掲載されている教科書があります。 (1
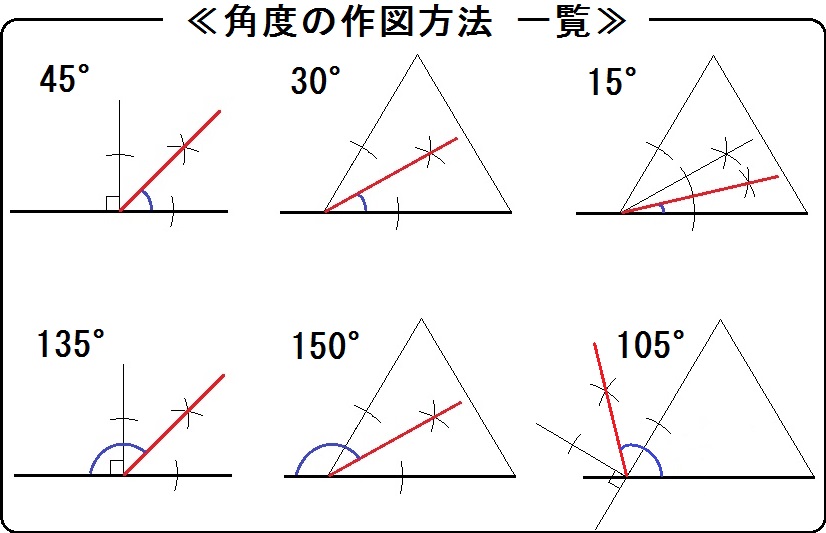
ボックルくん 105 最大100マスを使って四則演算を行い 内接円の作図、書き方とは それでは、次の三角形に内接する円を作図していきましょう。 角の二等分線をひいて、それぞれの交わる点を見つけます。 次は半径の大きさを調べます。 中心から、三角形の辺に向かって垂線をひきます。 中心と接点の長さ分度器の形である半円形を書き,中央に90度を示す垂線を書きます。 半円はできるだけ大きく書いたほうが作図しやすくなります。 60度を2等分して30度、さらに2等分して15度に印を付けます。 次に黄金直角三角形を作り、
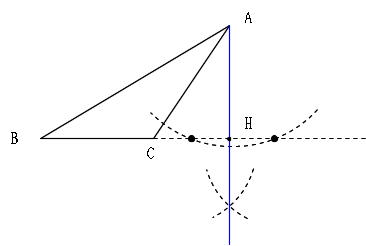



Mathematics 作図 1 作図の基本問題 働きアリ



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ
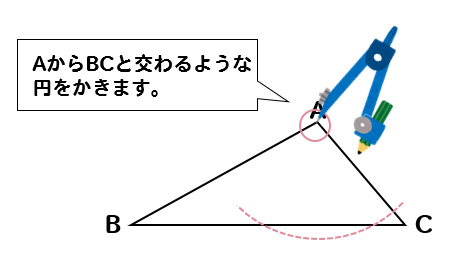
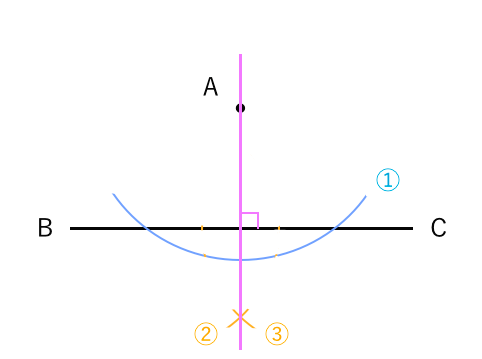
直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので,次の図で AH=DC になる. この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり, HC三角形の各頂点から対辺に下ろした垂線の足から、それぞれ他の2辺に下ろした垂線の足は1円周上にある ソフト詳細説明 ・三角形の各頂点から対辺に下ろした垂線の足 ( 図の D,E,F ) から、それぞれ他の2辺に下ろした垂線の足 ( 図の J K M N P Q の6点 ) は、1つの円周上にあります。 Cから半径ACの円弧をコンパスでAAあたりに描き、 Bから半径ABの円弧をAAあたりに描き、 ふたつの縁故が交差した点をAAとすると、 AとAAを結んだ線が、BCに直角になります (^^) 角Aの二等分線を間違って描く人が多いので、気をつけてくださいね★




作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ



三角形に接する円 中学から数学だいすき
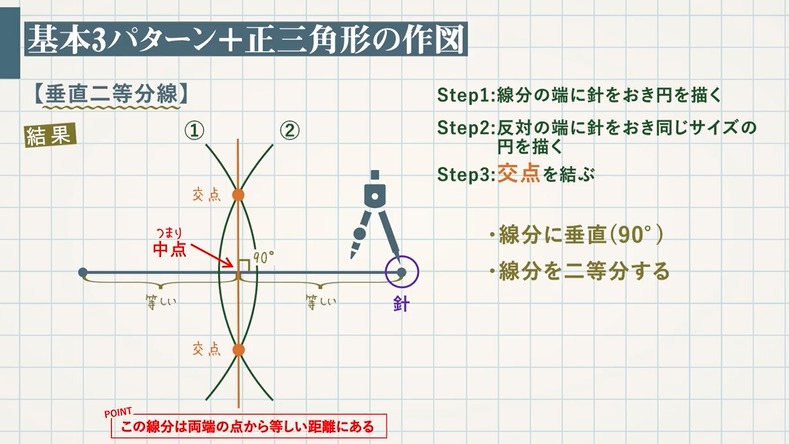
三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。 こんにちは、ウチダです。 今日は、中学1年生で習う 「垂直二等分線」 について、その作図方法とそれが正しいことの証明を解説したのち、実際に作図問題で練習し、最後に垂線の作図も考察していきます。 垂直二等分線の書き方 垂直二等分線とは、読んで字のごとく「垂直」で線分を「二 直角三角形は、垂線 bh=bc であるため、新たに垂線が引けない。 一つの角度が直角、つまり $90°$ であれば、鈍角の角度は作れない。 この $2$ つの理由から、直角三角形においては反例が作れなさそうですよね! ただ、「そもそもこれ以外に反例が存在しないこと」を示すのは困難です




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典
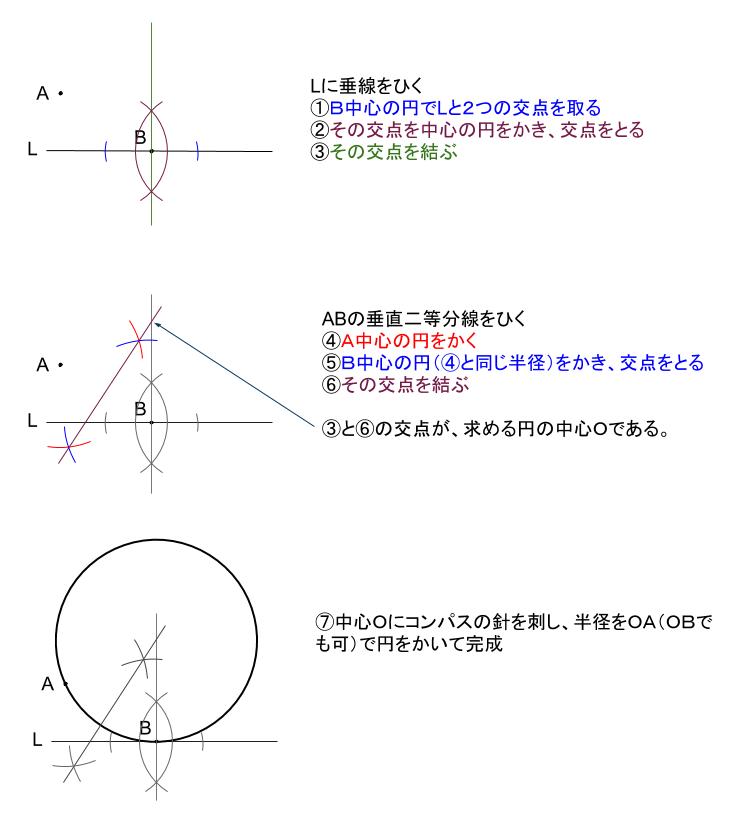
中心から、三角形の辺に向かって垂線をひきます。 すると、接点の場所がわかるので 中心と接点の長さを半径と 円の外部の点を通り円に外接する円の作図 円、円、言ってよくわかりませんが こうしろってことです。 やり方はいくつかありますが、いろんな問題に対応しやすいやり方を載日本大百科全書(ニッポニカ) 垂心の用語解説 三角形の三つの頂点からその対辺に下ろした三つの垂線は1点で交わる。その点を三角形の垂心という。鋭角三角形の垂心は三角形の内部にあり、直角三角形の垂心は直角の頂点である。また、鈍角三角形の垂心は、鈍角である頂角の対頂角の内部 正弦定理とその証明 数学 i 「図形と計量」で学習する正弦定理。 当たり前のように使っているかもしれませんが、そもそも正弦定理がなぜ成り立つのか、気にしたことはありますか? 学校の定期試験などでも、定理の証明が求められるかもしれません。 そこで今回は、正弦定理の証明を




垂線 の2通りの作図方法 コンパス 定規 数学fun
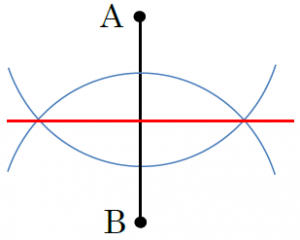



中1数学 垂直な線の作図のしかた まなビタミン
S:点aを通るbcの垂線を引く. S:点aを通るbcの中線を引く. S:bcの垂直二等分線を引く. S:点aを通るbcの平行線を引く. S: abcと合同な三角形を組み合わせる. S:手がなかなか動かない. ・平行線の性質を例に,逆についての学習 を想起させる. ・2つの角が等しい三角形の図を複数かい 三角形の各頂点から対辺に垂線をひきます。垂線は3本できますが、この3本の線は1点で交わります。 この点を、この三角形の垂心(orthocenter) といいます。 ただ、「3本の垂線が1点で交わる」ことは、自明なことではありません。以下では、座標を使ってこのことを考えてみましょう。スマートフォン 不等辺三角形 のAの角度を求める式が欲しいです。 8 0658 60歳以上 / 自営業 / 非常に役に立った / 使用目的 鉄工所を経営しているのですが、水路に架ける鉄板の寸法出しに役だてています。 現場合わせでの加工なので大変助かります。 9 01



垂線の応用 三角形の高さの作図 デジタル教科書 電子教科書



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ
長方形・正方形の書き方 方眼紙を使ってかく方法はすでに習っていますので ここでは方眼紙を使わず、ものさしと三角定規2枚を使って書く方法です。 動画作成協力・・動くイラストフリー素材 下の図 正三角形の書き方 次に、正三角形の書き方を次の例題で説明していきます。 例題 \(1\) 辺が \(3 \ \text{cm}\) の正三角形を作図しなさい。 正三角形は次の \(3\) つの手順で書くことができます。 STEP1 定規で底辺を書く 定規で \(3 \ \text{cm}\) をとり、底辺を書きます。 書いた底辺を線分 \(\mathrm{AB三角形の垂心の証明 / 数学A by となりがトトロ マナペディア 2 三角形の相似条件 nakagunttamainjp;



中学数学 平面図形




正三角形 の作図方法 コンパス 定規 数学fun
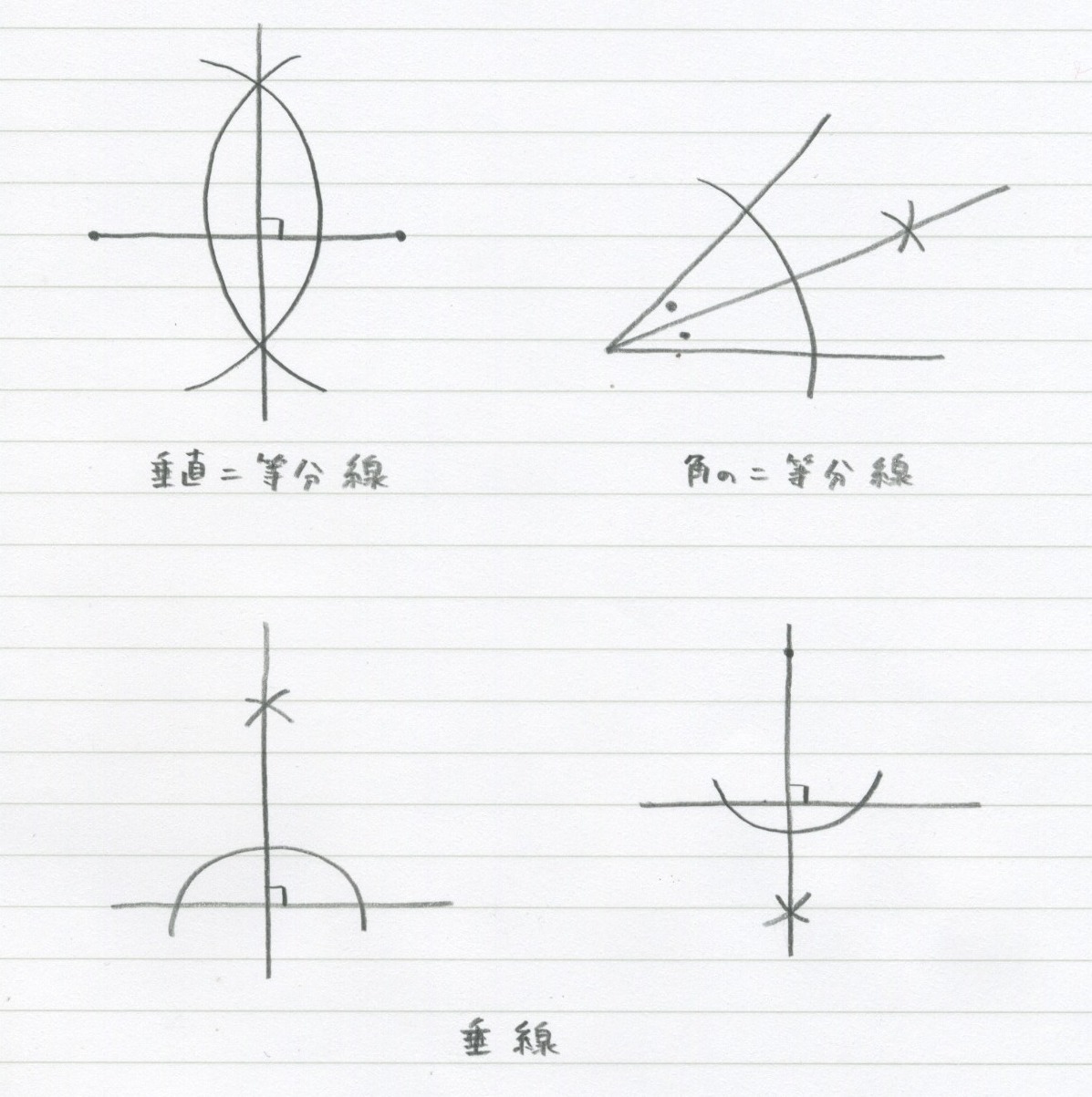
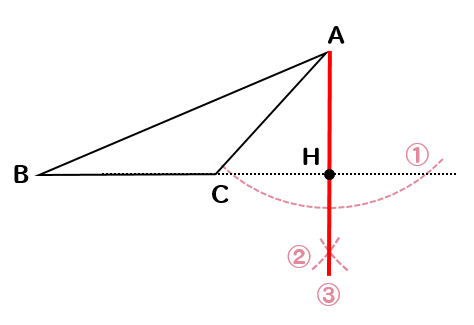
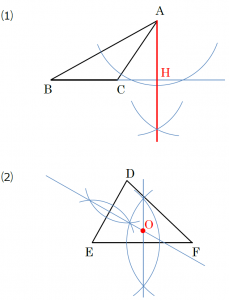
三角形の五心(重心・内心・外心・垂心・傍心)の作図方法まとめ! 21年2月19日 (垂線の引き方) ① 頂点から弧を描き、向かい合う辺と \(2\) つの交点を得る ② その \(2\) 交点から同じ大きさの弧を引き、交点を得る ③ 頂点からその交点に直線を引く \(2\) 本の垂線の交点が垂心となり三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 正三角形の底面積は,\ 三角比を用いた面積公式により直ちに求められる 実は,\ 本問は正四面体なので,\ 対称性を利用すると簡潔に済む 対称性より頂点から下ろした垂線の足は底面の重心なので,\ 計算せずともOH}={abc}{3}である




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト



Http Www Hyogo C Ed Jp Gimu Bo Gakuryokutyousa Kadai H28 07 28a41 Pdf
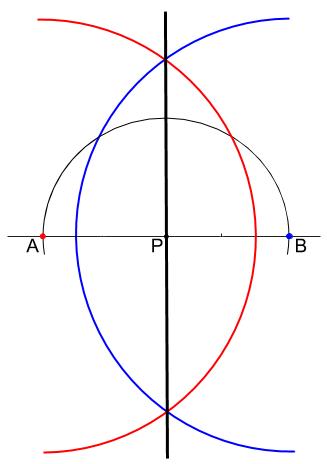
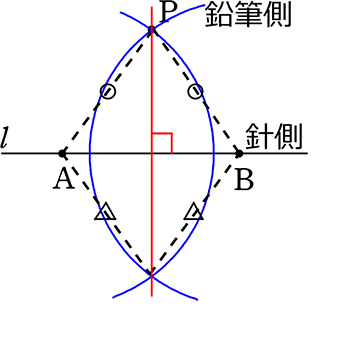
そのうち「直線上のある点を通る垂線」は、今回解説している「角の二等分線」の作図の一種と見ることができます。 作図手順は以下の通り。 点aを180°の角とみなすと、垂線はこれの二等分線となります。実際に作図の手順もほぼ同様です。 では、なぜこのように描いた線が角の二等分線に この新しくできた三角形a'b'c'が「回転移動した図形」だ! やったね! 疲れたー まとめ:回転移動の書き方はたった5つのステップである 回転移動の書き方はどうだった??? コンパス、三角定規、分度器っていう3つのアイテムでチョちょいのちょい。 >垂直二等分線の書き方 でも、なんでこのやり方で垂線ができるんだろう? 垂線の「なぜ」については、次の画像で確認してみましょう。 コンパスを使って円を作図していくことで、上のように2つの合同な三角形を作ることができました。(合同形も大きさもすべて同じ図形のこと



コンパスと定規を使った垂直線の描き方 図形の描き方001a 夏貸文庫




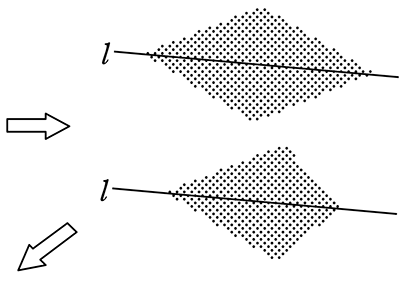
標準 平行移動に関する作図 なかけんの数学ノート



中学数学 垂線の作図 重要な2つ 中学数学の無料オンライン学習サイトchu Su
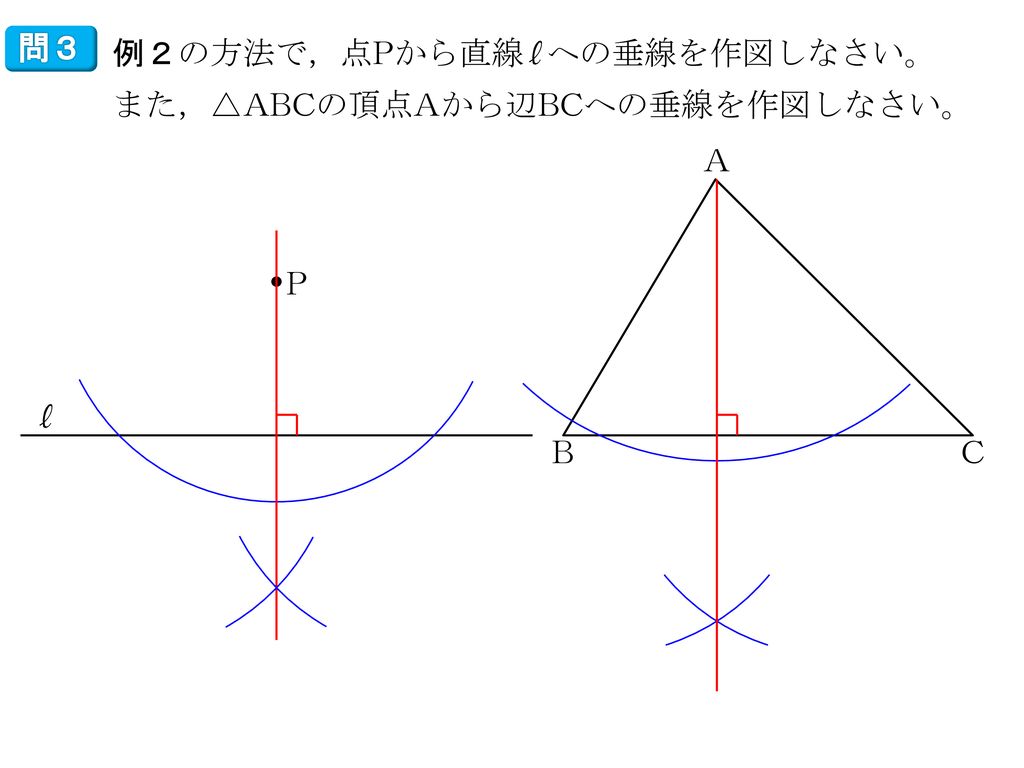



中学数学1年 5章 平面図形 2 作図 3時間 Ppt Download




応用 90度に関連する作図 なかけんの数学ノート




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



12 1 作図 結局4つ 勉強できようサイト



3



中1数学 垂直な線の作図のしかた まなビタミン



中学数学 作図 円と接線 接点 中学数学の無料オンライン学習サイトchu Su




テストでこんな問題が出ました Clear




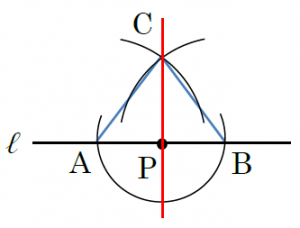
垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学



Q Tbn And9gcrd P2pctuz8gfkpppw9apzd Qqafrxhfweennrb5u0gatejnzy Usqp Cau



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図
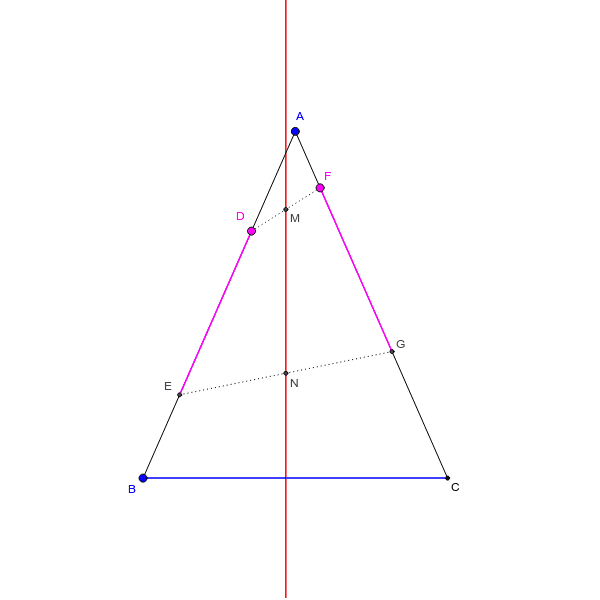



二等辺三角形と垂線 Geogebra




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




作図ー垂線 いろいろな問題 無料で使える中学学習プリント



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ



正三角形の書き方 高さが6センチの正三角形を描きたいです どのように描けば Yahoo 知恵袋




作図の3種類 垂直二等分線 角の二等分線 垂線 は 実は同じ図形だ 東大に文理両方で合格した男が綴る 受験の戦略



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく
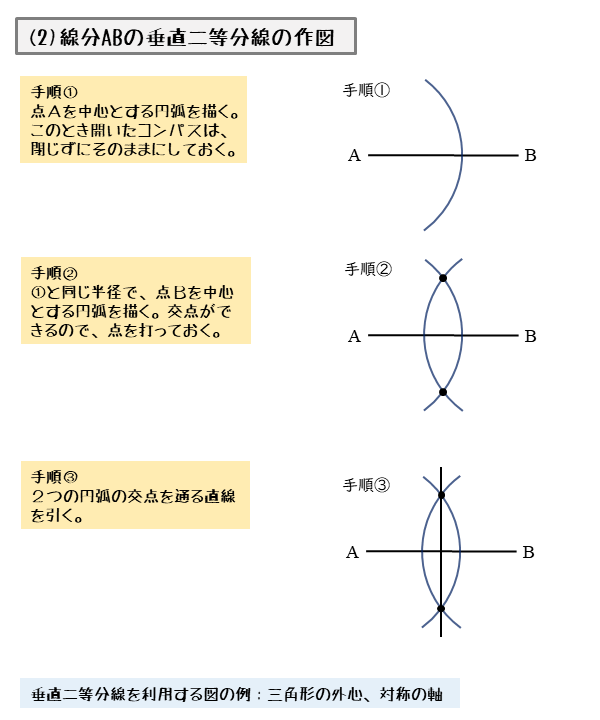



図形の性質 作図について 日々是鍛錬 ひびこれたんれん



垂線の応用 三角形の高さの作図 デジタル教科書 電子教科書
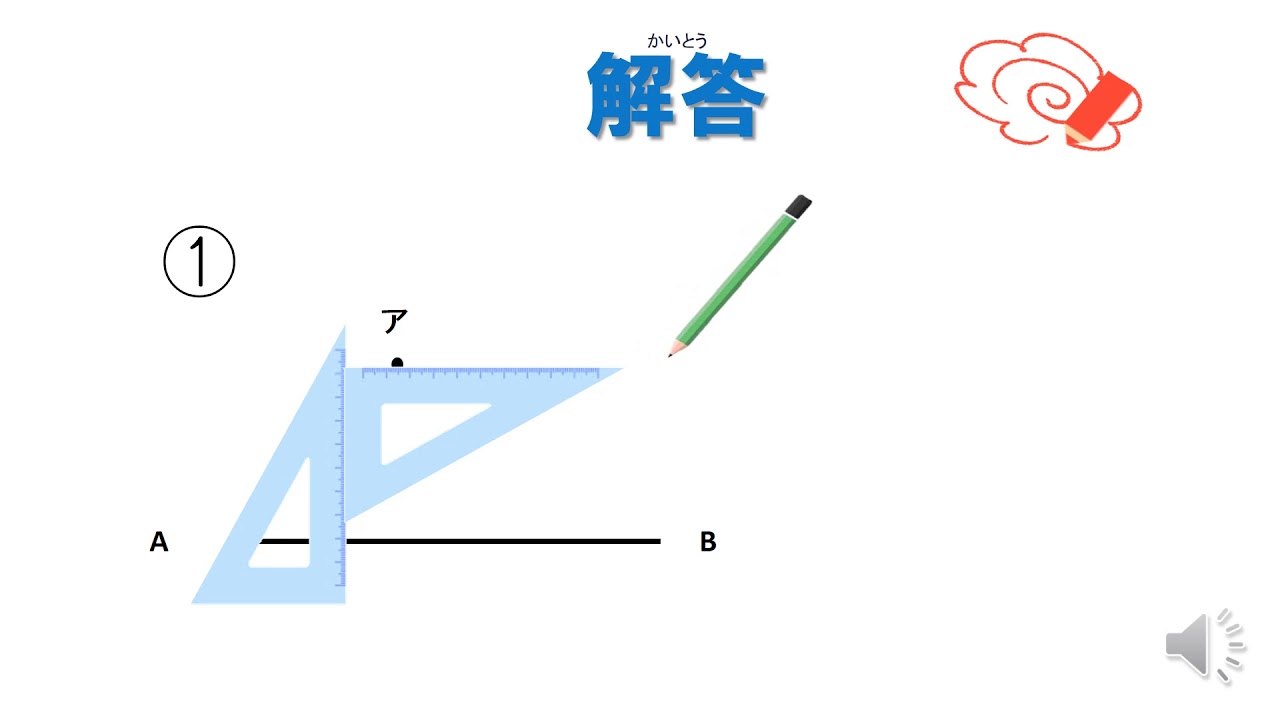



小3 平行線の書き方 三角定規 日本語版 Youtube




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく
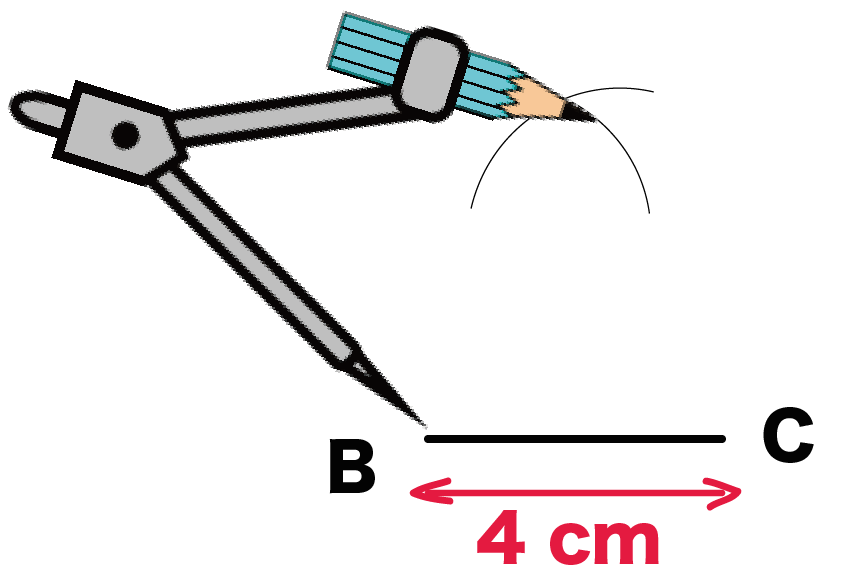



中学数学 二等辺三角形の書き方 作図がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
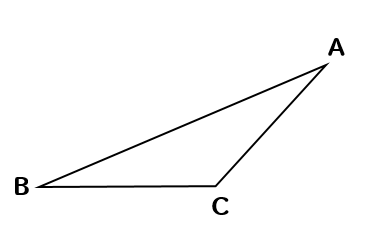



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ




垂線 の2通りの作図方法 コンパス 定規 数学fun



垂線の作図の証明




三角形の内接円の作図法と証明について 三角形の内接円の作図法と証明 数学 教えて Goo




垂線 の2通りの作図方法 コンパス 定規 数学fun




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



三角形の面積を二等分する 垂線 理系男子の独り善がり



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト




垂線 の2通りの作図方法 コンパス 定規 数学fun



垂心について



簡単にわかる 垂線を作図する方法 苦手な数学を簡単に



中1数学 垂直な線の作図のしかた まなビタミン



中学数学 垂線の作図 重要な2つ 中学数学の無料オンライン学習サイトchu Su



1



垂線 の2通りの作図方法 コンパス 定規 数学fun




中1 数学 平面図形8 垂線の作図 7分 Youtube
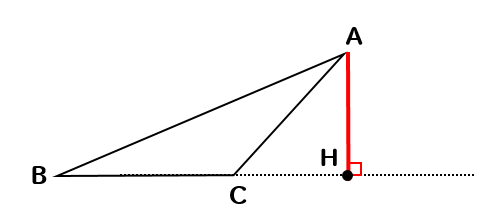



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ




垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学
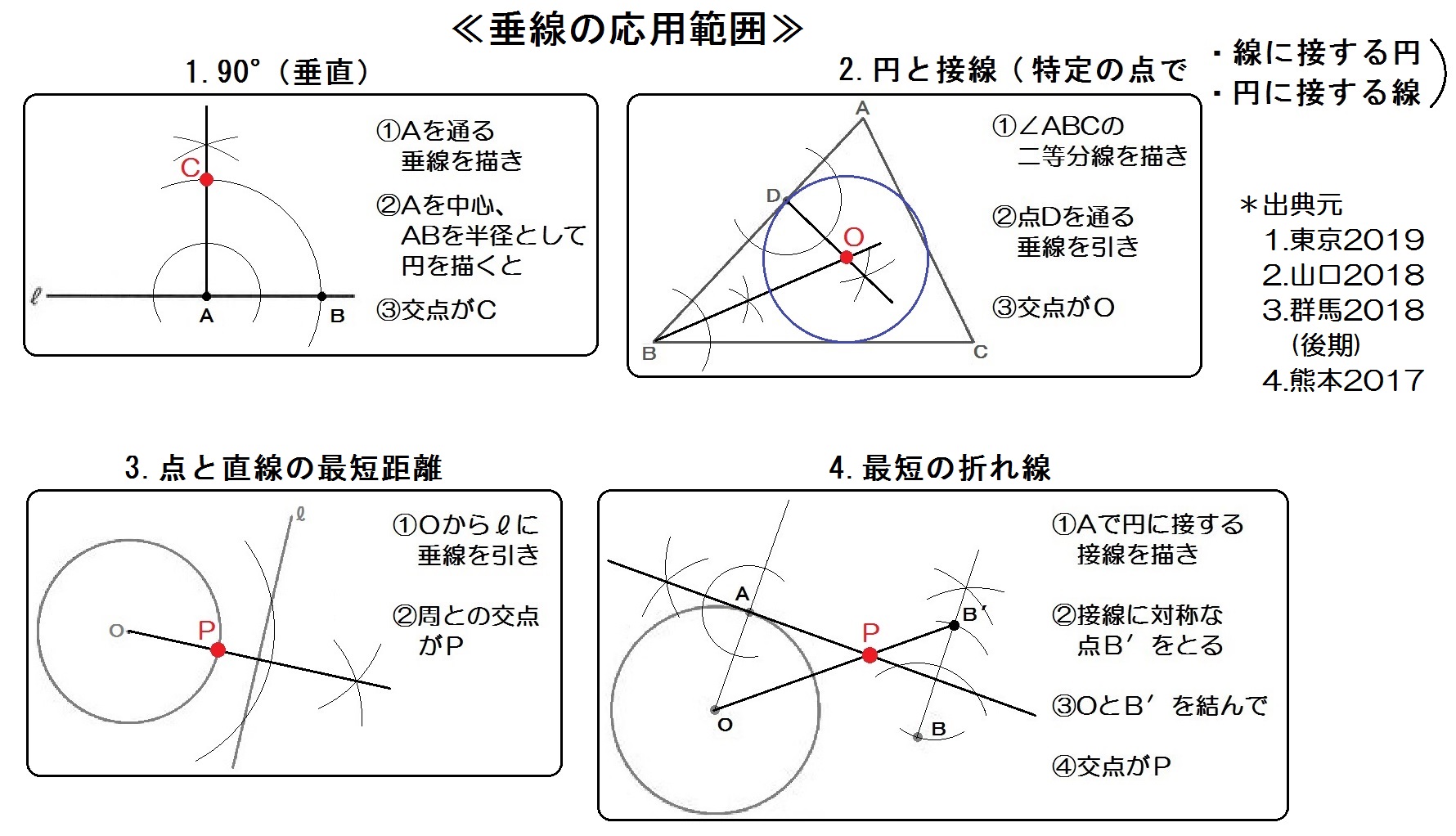



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図



数学の 作図問題 が苦手 得点源にするコツ教えます 高校入試よくでる 2 ベネッセ教育情報サイト



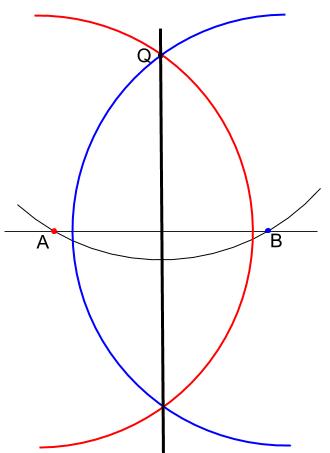
垂線の作図方法を教えて下さい 三角形abcで点aを通る直線bcの垂線の作 Yahoo 知恵袋



中学数学 平面図形




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




中2の数学の直角三角形の証明なのですが Clear




垂線 の2通りの作図方法 コンパス 定規 数学fun



雑学のソムリエ 平行線の作図



垂線の作図方法を教えて下さい 三角形abcで点aを通る直線bcの垂線の作 Yahoo 知恵袋



1年生で習う作図まとめ 教遊者



コンパスと定規を使った垂直線の描き方 図形の描き方001a 夏貸文庫



垂線の作図方法を教えて下さい 三角形abcで点aを通る直線bcの垂線の作 Yahoo 知恵袋




基本の作図について 承前 中学数学教材研究ノート




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



中学数学 垂線の作図 重要な2つ 中学数学の無料オンライン学習サイトchu Su




証明の書き方で最初に と において と書く時 Clear



垂線の作図方法を教えて下さい 三角形abcで点aを通る直線bcの垂線の作 Yahoo 知恵袋



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学
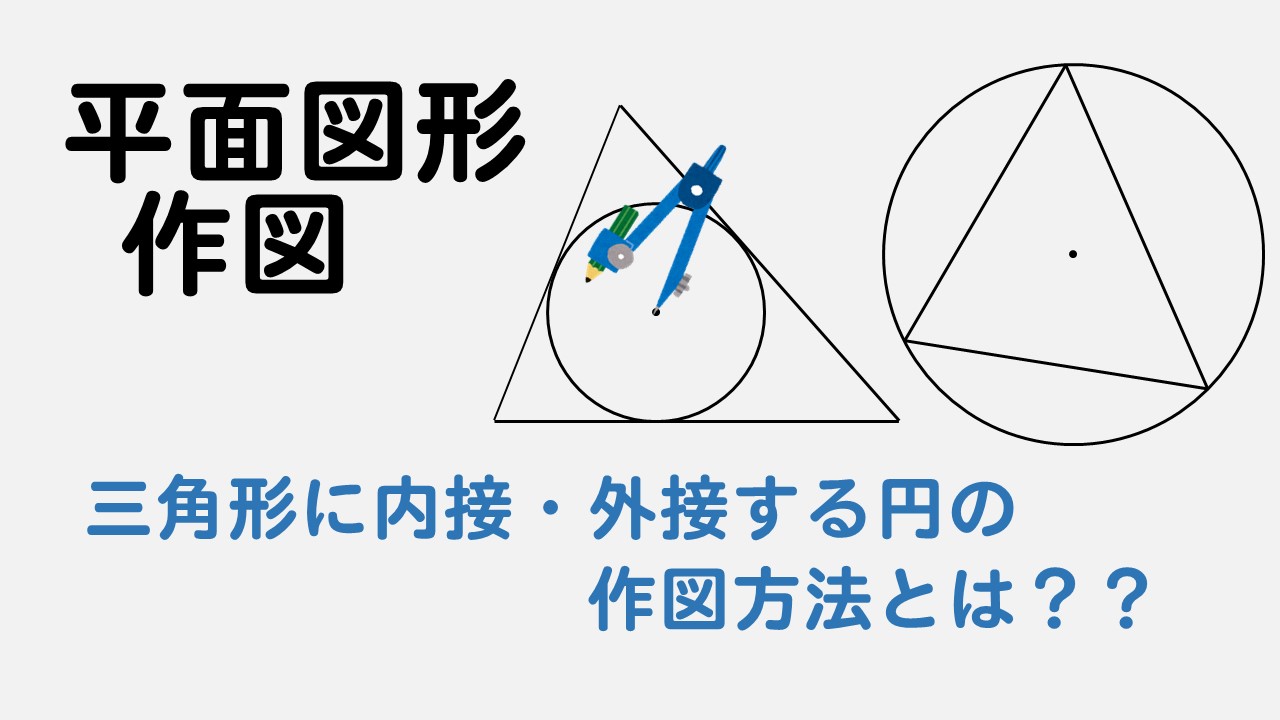



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ




垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学
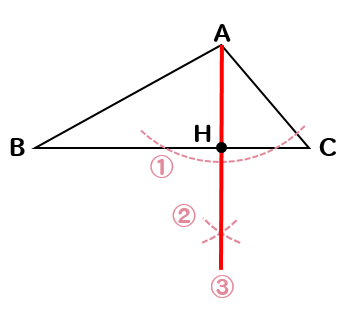



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト




懐かしの数学作図 直線上の点pを通る垂線を引く の作図問題を コンパスを1回だけ使って 解く 圧倒亭グランパのブログ




垂線 の2通りの作図方法 コンパス 定規 数学fun



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




垂線の書き方 作図 中学1年数学 Youtube




標準 75度や150度の作図 なかけんの数学ノート
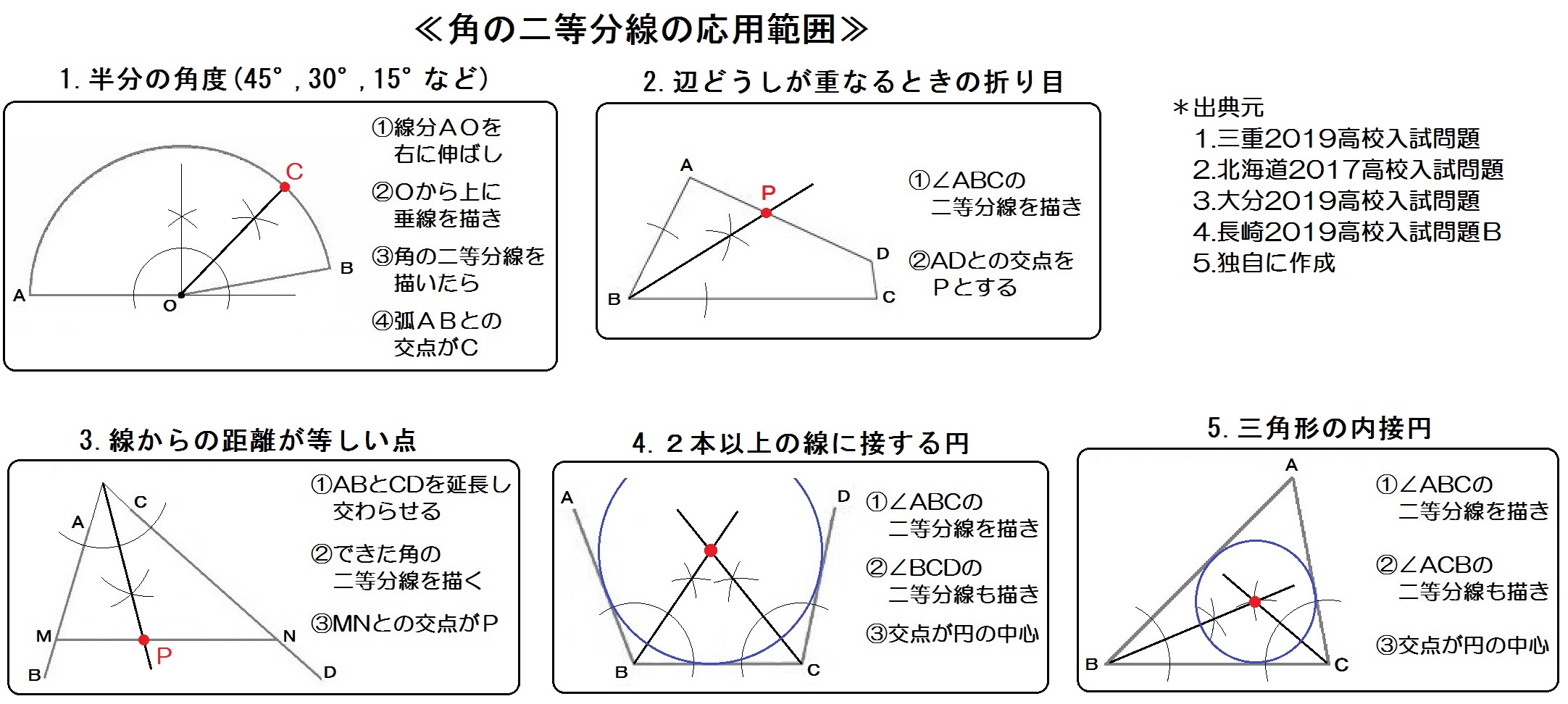



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




Aを頂点のひとつと Bがpqの中点になる正三角形apqの作図の問題です Clear
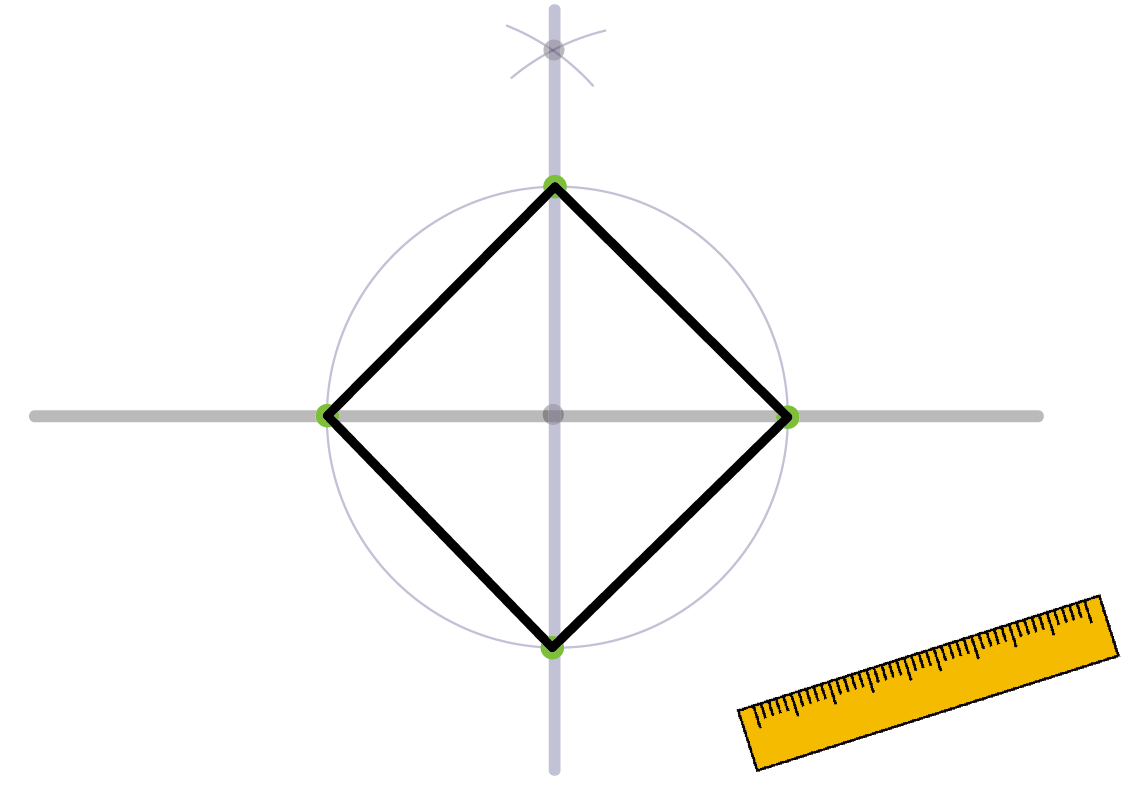



コンパスで作図 正方形の書き方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく
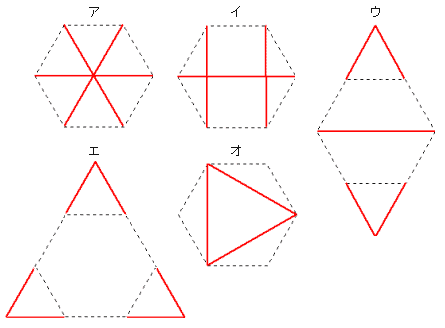



課題学習の指導 数学



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




三角形の垂心について知っておきたい知識まとめ 理系ラボ



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ
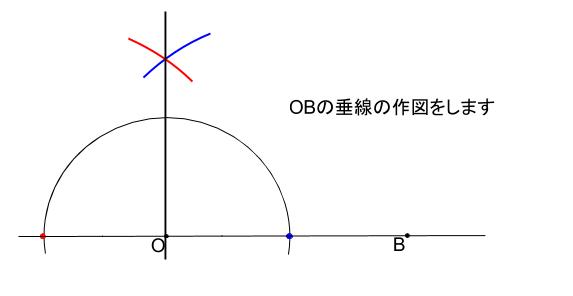



中学数学 作図 30 45 有名角の作図 中学数学の無料オンライン学習サイトchu Su




垂線 の2通りの作図方法 コンパス 定規 数学fun




標準 75度や150度の作図 なかけんの数学ノート




垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学



0 件のコメント:
コメントを投稿